エリオット波動解説(第九回)フィボナッチについて解説
今回はエリオット波動におけるフィボナッチについて説明します。まず、フィボナッチとは何かということからしっかり確認しておきましょう。
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610・・・・・・・
という無限に続く整数の数列があります。1 1から始まって、隣り合う2つの整数の和が次の項になる数列です。
1+1=2 1+2=3 2+3=5 3+5=8 5+8=13・・・・・・
となっているのが確認できますね。この数列のことをフィボナッチ数列と言います。フィボナッチ数列のことをフィボナッチ級数と説明しているウェブサイトもあるようですが、それは明らかな誤訳です。「級数」とは数列の項の和を指しますから全く意味が違ってきます。用語は正しく覚えましょう。
そして、フィボナッチ数列の項として現れる整数のことをフィボナッチ数と言います。1 2 3 5 8 13 21 34 55 89 144などの数字のことです。また、フィボナッチ数同士の割合のことをフィボナッチ比率と言います。
隣り合う大きい方の数字を小さいほうの数字で割ってみましょう。
例えば、34÷21=1.619047619・・・です。
- 144÷89=1.617977528・・・
- 610÷377=1.618037135・・・
このようにほぼ1.618になっています。
逆に小さいほうの数字を大きい方の数字で割ると
- 21÷34=0.617647058・・・
- 89÷144=0.61805555・・・
- 377÷610=0.618032786・・・
とほぼ0.618になります。この1.618と0.618が代表的なフィボナッチ比率ということになります。
また、1つ間を空けた項同士の比率は、たとえば
- 610÷233=2.618025751・・・
- 233÷610=0.381967213・・・
というように約2.618や0.382になります。
2つ間を空けた項同士では、たとえば
- 610÷144=4.236111111・・・
- 144÷610=0.236065573・・・
と、約4.236や0.236になります。このように0.618や1.618の他に0.236、0.382,2.618、4.236もフィボナッチ比率です。
また、0.618や1.618は黄金比とも呼ばれます。これは1202年にレオナルド・フィボナッチがフィボナッチ数という概念を発表するずっと前の紀元前3世紀ころにユークリッドによって外中比として発見されていました。
図84

外中比とは図84のように線分ABをAB:AP= AP:PBになるように分けた時のAPとPBの比率のことを言います。これを数式で表すと次のようになります。
AP=x、PB=1とすると、(x+1):x=x:1、x²=x+1、x²-x-1=0となり、xを2次方程式の解の公式にあてはめるとx=(1±√5)/2、x≧0なのでx≒1.618になります。
つまり、点Pは線分ABを1.000:0.618に分けることになるのです。1.000:0.618とは0.618:0.382のことです。
ラルフ・ネルソン・エリオットは著書「自然の法」のなかで、フィボナッチ数が自然や人間活動を大きく支配していると述べています。
その一例として、ピアノの1オクターブは8の白い鍵盤と5の黒い鍵盤の計13からできていることや、ギザのピラミッドの底辺が783.3フィート、高さが484.4フィートでその比率が0.618であり、高さの484.4フィートとはすなわち5813インチで、それは5と8と13というフィボナッチ数からなっていることなどを挙げています。
エリオット波動においては、インパルスは5波動からなっていて、続く修正波は3波動で、合計は8波動ですが、この5や3や8もすべてフィボナッチ数列です。インパルスの副次波は5波動、3波動、5波動、3波動、5波動ですが、これらの波動を合計すると21というフィボナッチ数になります。さらに一回り大きな波動は89の波動から構成されていてこの89もフィボナッチ数です。
このようなことから、エリオット波動原理では、波動もフィボナッチ数やフィボナッチ比率に支配されていて、波動同士、中でもアクション波同士はフィボナッチ比率の関係になると考えられています。以下にエリオット波動でよく使われるフィボナッチ比率を波形ごとに挙げてみます。
まずはインパルスです。
図85
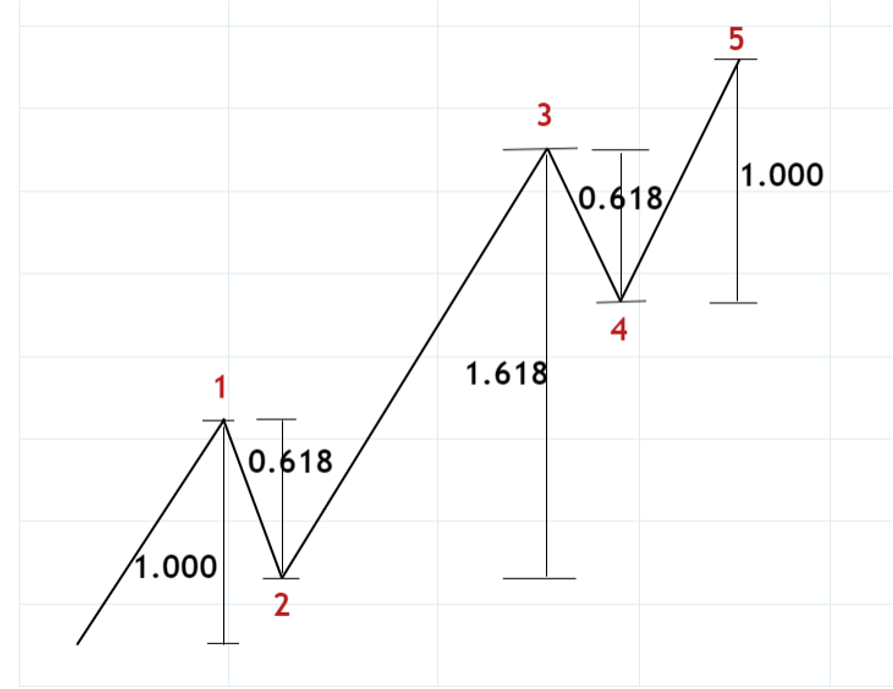
1波の大きさを1.000とすると、2波はその0.618を修正するというガイドラインがあります。3波は1波の1.618倍になるのが理想とされ、4波は3波を0.382修正しますから1波の1.000に対しては0.618ということになります。また、5波は1波と同じ1.000となるのが理想です。
また、図86のように4波終点の位置でインパルス全体を黄金比率に分けること(黄金分割)も理想とされています。
図86
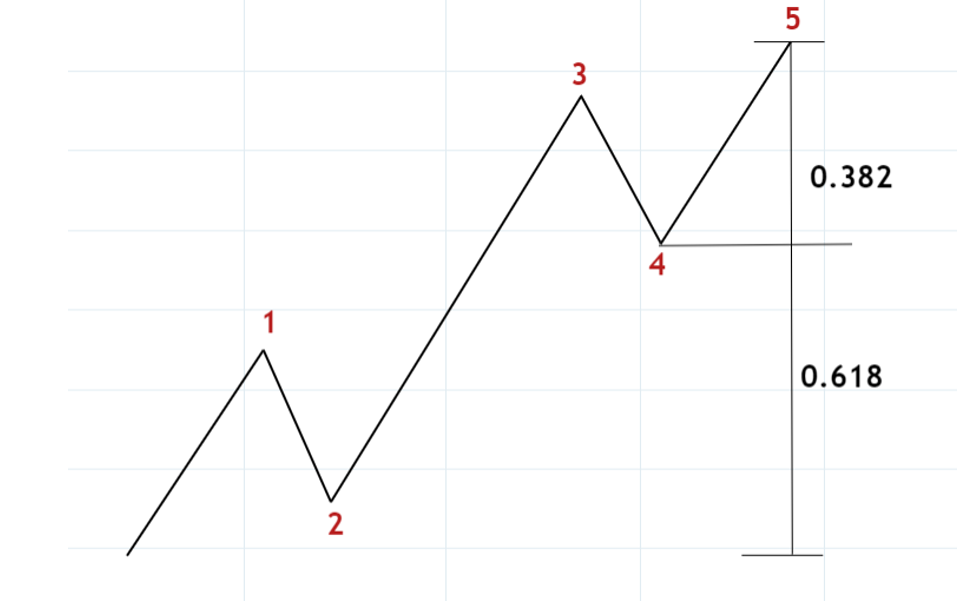
次にジグザグです。
図87
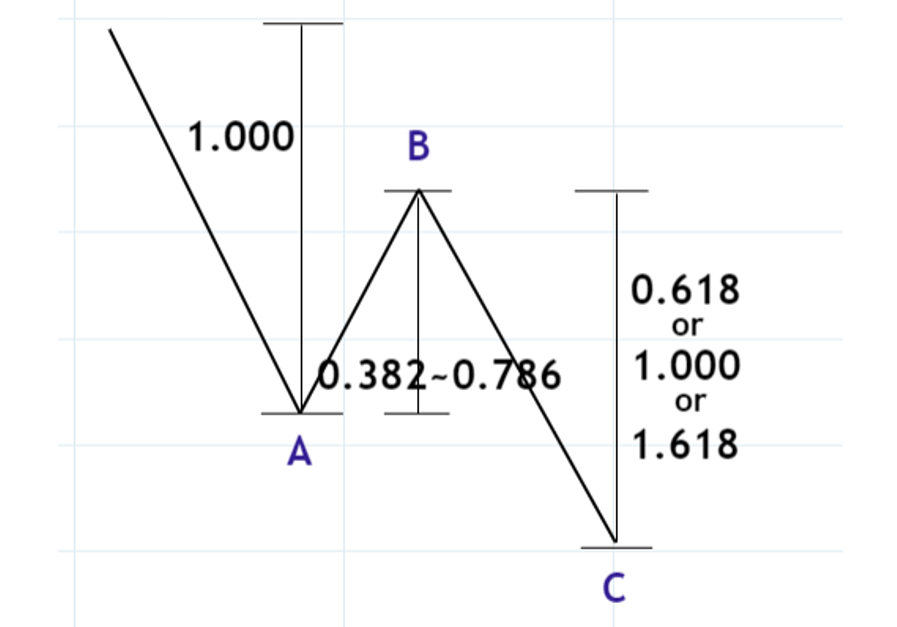
A波を1.000とすると、B波はA波を0.382から0.786修正すると言われています。0.786とは0.618の平方根ですがフィボナッチ比率ではありません。また、C波はA波と同じか0.618倍または1.618倍になるのが理想です。
フラットの波動同士の比率は次のようなものが目安となります。
図88
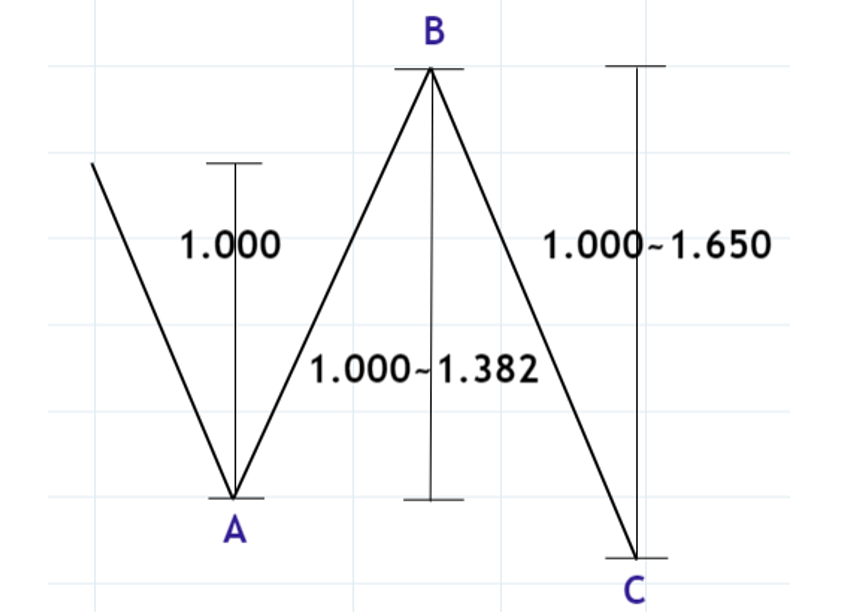
A波の大きさを1.000とすると、B波は一般的には1.000の大きさになります。拡大型フラットではB波はA波の1.236から1.382の大きさになるのが理想です、1.236や1.382はフィボナッチ比率ではありませんが、フィボナッチ比率である0.236や0.382だけA波より大きくなるという解釈です。また第七回でも説明しましたが、B波は最低でもA波を90%以上リトレースする必要があります。
C波はA波の1.000から1.650の大きさになるのが目安とされています。1.618でない理由はよく分かりませんが「ELLIOTT WAVE PRINCIPLE」の記述を参考にしました。
最後にトライアングルですが波動同士は次のようなフィボナッチ比率になることが多いとされています。
図89
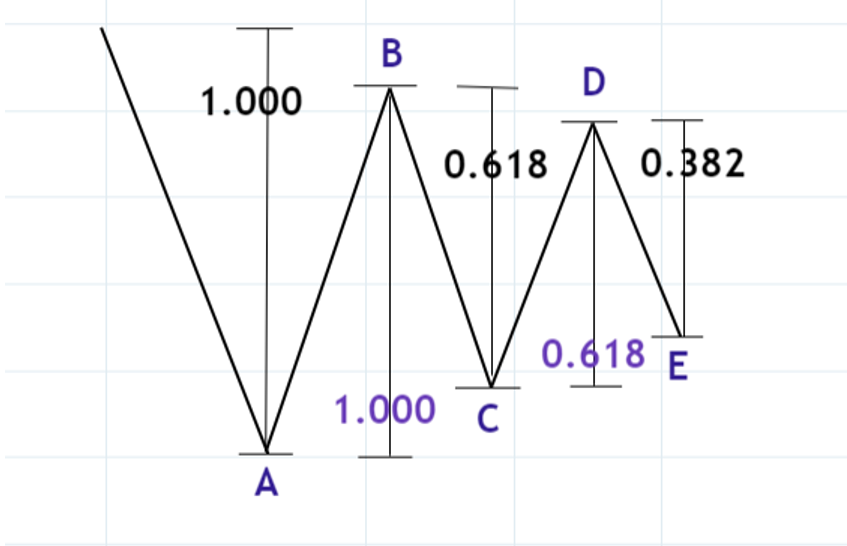
これは、全ての副次波がこのような比率になるという意味ではなく、A波とC波、C波とE波、もしくはB波とD波のいずれか一つが1.000:0.618になるということです。
エリオット波動原理では波動同士の比率に関して以上のようなガイドラインがありますが、いずれも「そのようになるのが望ましい」とか「そうなることを仮定して予想を立てましょう」という意味と捉えた方がいいでしょう。実際にはそのような比率関係が見られないことの方がむしろ多いからです。
また、ラルフ・ネルソン・エリオットは「自然の法」のなかで、強気相場や弱気相場の継続年数が3年や5年、13年、21年といったフィボナッチ数になっている事例を幾つも挙げています。
第九回は以上です。
次回の最終回では、実際に波動をカウントする手順について解説します。
一般社団法人エリオット波動研究所代表理事 有川和幸氏監修
この記事を監修してくださった有川和幸氏と小泉秀希氏の共著「あなたのトレード判断能力を大幅に鍛えるエリオット波動研究 基礎からトレード戦略まで網羅したエリオット波動の教科書(パンローリング社) 」には更に詳しくエリオット波動について説明されています。
エリオット波動についてもっと学びたい方へのオススメ

一般社団法人エリオット波動研究所代表理事の有川和幸(ありかわかずゆき)氏監修のもとエリオット波動の基本的な知識や使い方、トレーディングアイデアなどをご紹介。またエリオット波動へ応用が可能なOANDAオリジナル・インジケーター「OANDA_Auto_fibonacci(オート・フィボナッチ)」を無料配布中。このインジケーターはOANDAの口座をお持ちのお客様だけがお使いいただけます。
本ホームページに掲載されている事項は、投資判断の参考となる情報の提供を目的としたものであり、投資の勧誘を目的としたものではありません。投資方針、投資タイミング等は、ご自身の責任において判断してください。本サービスの情報に基づいて行った取引のいかなる損失についても、当社は一切の責を負いかねますのでご了承ください。また、当社は、当該情報の正確性および完全性を保証または約束するものでなく、今後、予告なしに内容を変更または廃止する場合があります。なお、当該情報の欠落・誤謬等につきましてもその責を負いかねますのでご了承ください。











