ボリンジャーバンドの基礎となる標準偏差とは?計算方法も紹介
1.ボリンジャーバンドの計算方法
ボリンジャーバンドの上下バンドは、中央の移動平均線(Simple Moving Average:SMA)に標準偏差(σ)を加減したものです。以下の簡単な計算により求められます。
| ±1σ | 単純移動平均±標準偏差 |
|---|---|
| ±2σ | 単純移動平均±標準偏差×2 |
| ±3σ | 単純移動平均±標準偏差×3 |
この計算で用いる標準偏差は統計学で用いられる考え方です。平方根を使うなど計算方法はやや複雑ですが、簡単に言うとデータ(終値)が平均値からどれくらい散らばっているかを表します。
標準偏差の計算式
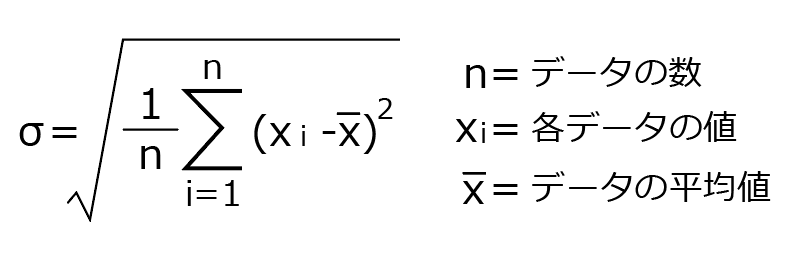
ボリンジャーバンドにおいてこの標準偏差が表すのは、直近n期間の各終値が、n期間のSMAからどれくらい散らばっているかということです。SMAから離れた終値が多ければ標準偏差は大きくなり、SMAに近い終値が多ければ標準偏差は小さくなります。この性質がバンド幅の拡大や縮小になって現れます。
2.統計学の正規分布の考え方
統計学の正規分布では、データは次の確率で各標準偏差の範囲に分布すると考えます。
| ±1σ | 68.26% |
|---|---|
| ±2σ | 95.44% |
| ±3σ | 99.74% |
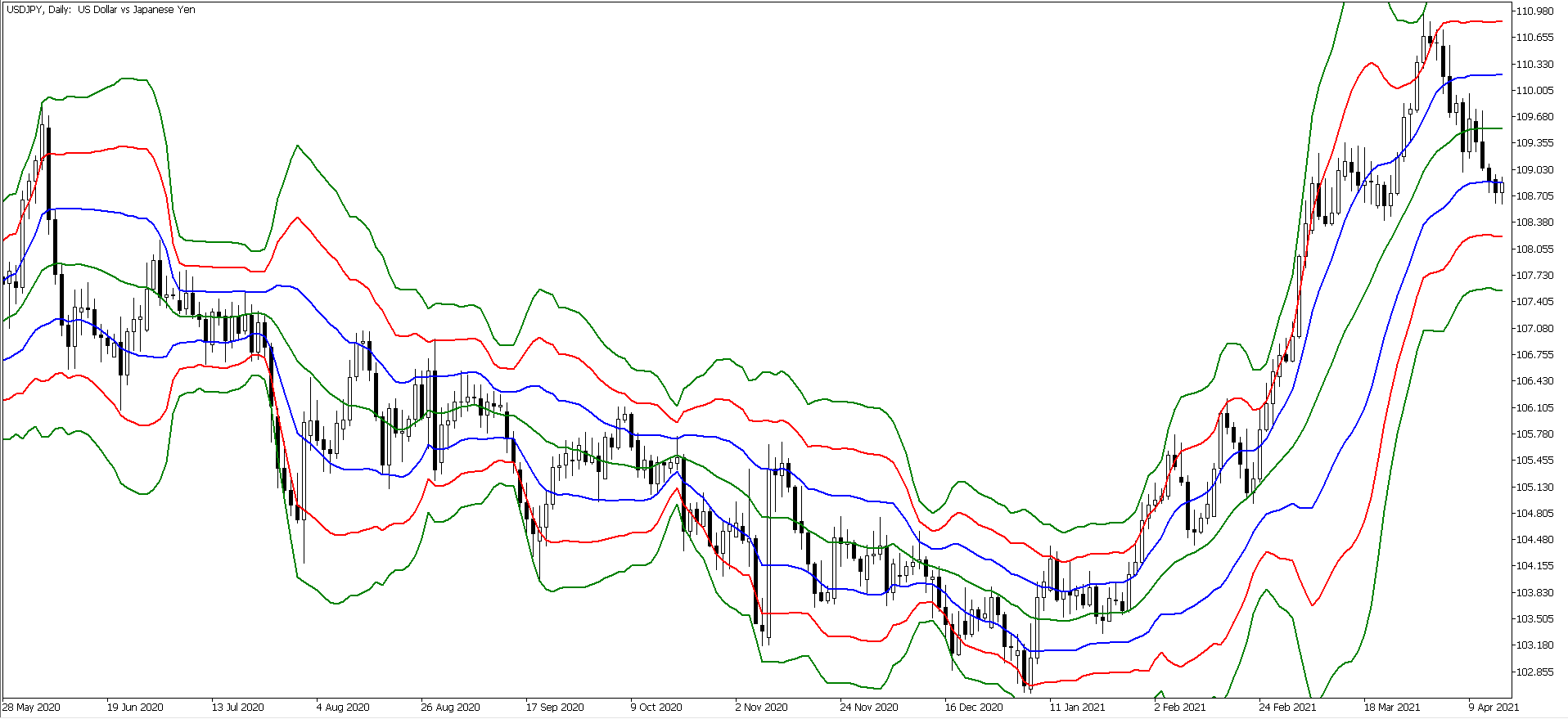
これをボリンジャーバンドに用いた場合、例えば「+2σと-2σの間には、終値の95.44%が収まる」という意味を表します。画像1を見ると分かるように、終値が±2σの範囲外に出るのはわずかなことです。また、±2σのバンドに到達しているということは、価格が相対的に高い(安い)と判断することができます。
±1σ(青)、±2σ(赤)、±3σ(緑)のバンドとローソク足の位置関係を見ると、上表の確率通りに終値が収まっている様子が分かるでしょう。
画像1/ローソク足の値動きと各バンドの範囲
3.標準偏差が表す確率の注意点
正規分布の確率について、注意したいことがあります。ボリンジャーバンドはあくまでも過去の終値から標準偏差を求め、それぞれの終値が正規分布の確率でバンド内に収まるよう描かれているに過ぎず、未来の終値がバンド内に収まる確率を表すわけではないのです。
±2σの範囲外で終値が連続することは、決して珍しいことではありません。強いトレンドが発生している局面では、±2σの範囲を連続で抜け出すパターンが見られます。画像2では、バンドウォーク(±2σに沿うようローソク足が推移すること)と呼ばれるトレンド継続の特徴的な形が現れており、この局面ではローソク足の終値が連続して+2σの外側で終値をつけているのが分かります。
画像2/バンドウォークでは終値が連続して±2σを抜け出す
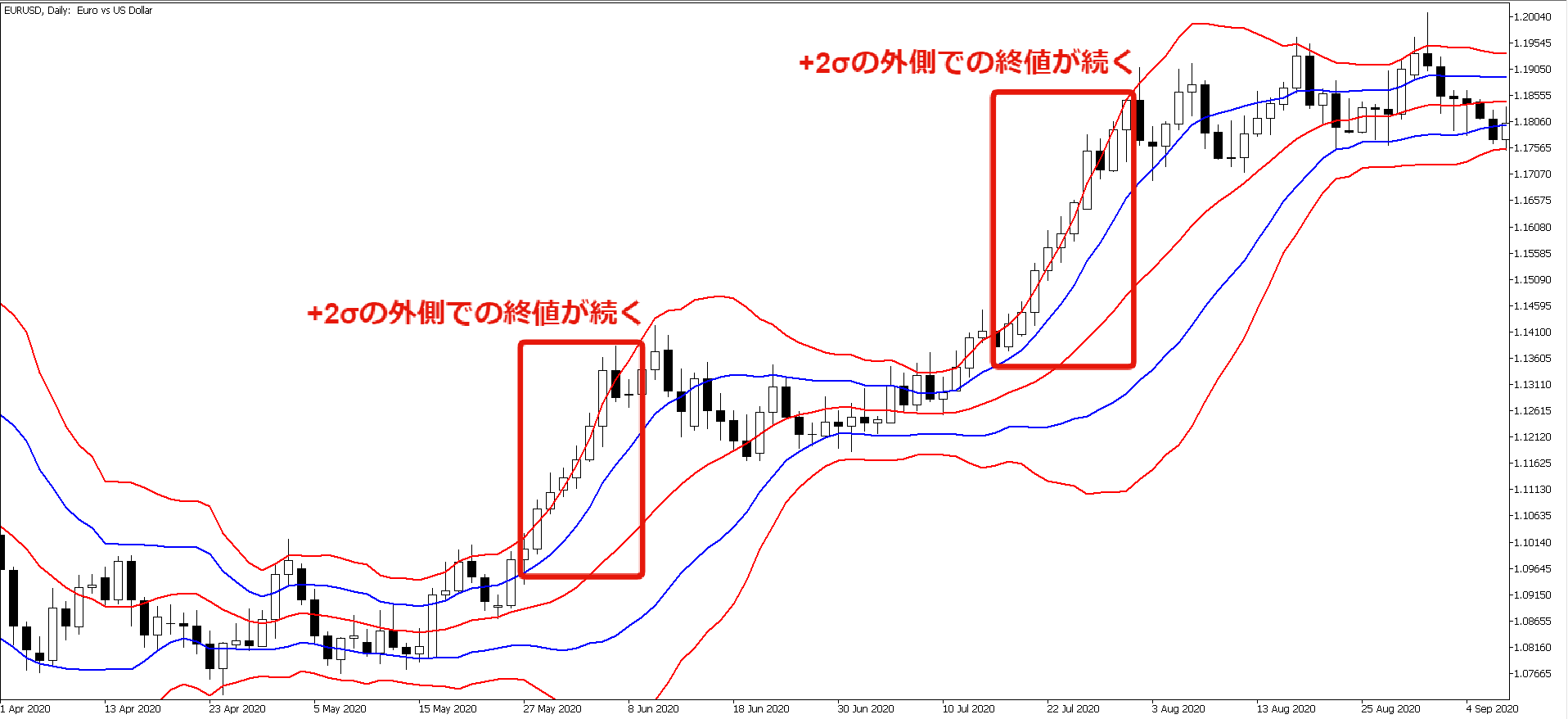
こうした性質があることから、ローソク足がボリンジャーバンドの±2σ(±3σ)に達した際、単純に買われ過ぎ/売られ過ぎだと判断するのは早計です。決して逆張りのサインとなるわけではなく、むしろトレンドが順行する可能性が強いと言えます。ローソク足の推移とバンドの形状の両方を見て、トレンドの判断をするのが重要です。
監修:山中康司氏
ボリンジャーバンドについてもっと学びたい方へのオススメコンテンツ
長く為替トレーディングの第一線で活躍されてきた山中康司(やまなかやすじ)氏監修のもと、ボリンジャーバンドの基本的な知識や使い方、トレーディングアイデアなどをご紹介します。またOANDAでは、ボリンジャーバンドに関するオリジナルインジケーターを多数提供しています。このオリジナルインジケーターは、OANDAの口座をお持ちのお客様だけがお使いいただけます。
本ホームページに掲載されている事項は、投資判断の参考となる情報の提供を目的としたものであり、投資の勧誘を目的としたものではありません。投資方針、投資タイミング等は、ご自身の責任において判断してください。本サービスの情報に基づいて行った取引のいかなる損失についても、当社は一切の責を負いかねますのでご了承ください。また、当社は、当該情報の正確性および完全性を保証または約束するものでなく、今後、予告なしに内容を変更または廃止する場合があります。なお、当該情報の欠落・誤謬等につきましてもその責を負いかねますのでご了承ください。

















