階層的リスクパリティによるポートフォリオの構築について
この記事ではポートフォリオの最適化について解説します。
ポートフォリオを組む目的は、複数の株などの資産を同時に保有したり、複数の損益の異なる取引戦略を同時に運用することでリスクを分散させることです。
つまり、複数の戦略がそれぞれドローダウンを打ち消し合って、全体的に安定した運用ができることに期待しています。
構成比率を変えることの影響
一つのMT5口座で、複数のEAを同時に稼働させることを想定してみます。
グラフは3つの戦略のパフォーマンスを想定したものです。

3つの戦略はそれぞれドローダウンを経験しつつも最終的には利益が残っています。
グラフを大まかに見てみると、前半のパフォーマンスが良かった戦略と、後半のパフォーマンスが良かった戦略があることがわかります。
この3つの戦略に、口座の運用資金を均等に3分の1ずつ割り当てたときのポートフォリオのパフォーマンスが、下グラフの青線になります。

単純に3分の1ずつ割り当てただけでも、ポートフォリオのパフォーマンスは3つの戦略それぞれ単体のパフォーマンスよりも上下の振れ幅は少なくなっていることが、視覚的に確認できるかと思います。
しかし、3つの戦略のうち2つは、後半期間に長めの停滞やドローダウンがあるため、ポートフォリオのパフォーマンスも後半がとくに伸び悩んでいる様子がわかります。
次に、単純に3分の1ずつ割り当てるのではなく、戦略同士のリターンがどれくらい類似しているかを考慮してポートフォリオの構成比率を変更してみます。
円グラフは構成比率を変更したイメージです。

再びポートフォリオのパフォーマンスを確認します。
青線は先ほどの3分の1ずつ均等に割り当てたポートフォリオで、赤線は新たに調整したポートフォリオです。(具体的な割り当ての計算方法については、あとで詳しく解説します。)

構成比率を調整した赤線のポートフォリオは、伸び悩んでいた後半期間のパフォーマンスが改善しています。
このように、同じ戦略を組み合わせたポートフォリオでも、構成比率によってパフォーマンスは変化します。
ただし、パフォーマンスが向上する構成比率を、損益が確定してから決定するのは、現実的な検証になっていないことに注意する必要があります。
過去のパフォーマンスを上げる構成比率ではなく、将来に起こるリスクを分散するための構成比率を求める必要があります。
次は、構成比率を求める、具体的なアプローチを説明します。
平均分散アプローチ
ハリー・マーコウィッツの平均分散は、最も有名なポートフォリオの最適化アプローチの一つです。
この考え方では、ポートフォリオを運用するときのリスクを、リターンの分散(または標準偏差)とします。
リターンの分散が大きいと不安定な収益となり、ポートフォリオ内のいくつかの戦略のドローダウン期が重なったときに、大きな損失になることも懸念されます。
ポートフォリオのリターンの平均が同程度なら、リターンの分散は小さくなるような構成比率を求め、またポートフォリオのリターンの分散が同程度なら、リターンの平均は大きくなるような構成比率を求めるというのが、このアプローチの狙いとなります。
様々な構成比率でのシミュレーション
イメージを掴むための例として、3つのアセット(またはEAのような戦略)を運用する仮定で考えます。
ポートフォリオ内のアセットの数と、同じだけ乱数を生成します。
この場合は、アセットが3つあるとしているため、生成する乱数は3つです。
3つの乱数rnd_1, rnd_2, rnd_3を使って、下記のようにw_1, w_2, w_3を求めます。
![]()
w_1, w_2, w_3は合計で1となるような、ランダムに割り当てた構成比率を示しています。
w_1, w_2, w_3を3つのアセットの過去のリターンにかけて、ポートフォリオのリターン(平均)とリスク(標準偏差)を計算します。
これを繰り返すことで、ランダムに構成比率を割り当てたポートフォリオを、無数に生成することができます。
ポートフォリオ内の各アセットの週次リターンを入れたデータフレームweekly_returnsから、重みweights(ランダムに割り当てた構成比率)によるシミュレーションを行うためのPythonコードの例です。
※記事中のPythonコードは、対象となる任意のポートフォリオの週次リターン(必ずしも週次である必要はありません)をデータフレームに入れたweekly_returnsが、あらかじめ定義されていることを前提としています。
import numpy as np
rf_rate=0
NUM_PF = 10000
mean_ret = weekly_returns.mean()
n_obs, n_assets = weekly_returns.shape
periods_per_year = round(weekly_returns.resample('A').size().mean())
alpha = np.full(shape=n_assets, fill_value=1/n_assets)
weights = np.random.dirichlet(alpha=alpha, size=NUM_PF)
r = (weights @ mean_ret.values + 1) ** periods_per_year - 1
sd = (weights @ weekly_returns.T).std(1) * np.sqrt(periods_per_year)
simul_perf= pd.DataFrame({'Annualized Standard Deviation': sd, 'Annualized Returns': r})
このコードでは、乱数を用いて10,000個のポートフォリオの年率リターンと年率リスク(リターンの標準偏差)をsimul_perfに入れています。
このように、無数に生成したポートフォリオの年率リターンの平均と年率リターンの標準偏差をグラフ化すると、特徴的な横向きの傘のような形状になることが知られています。
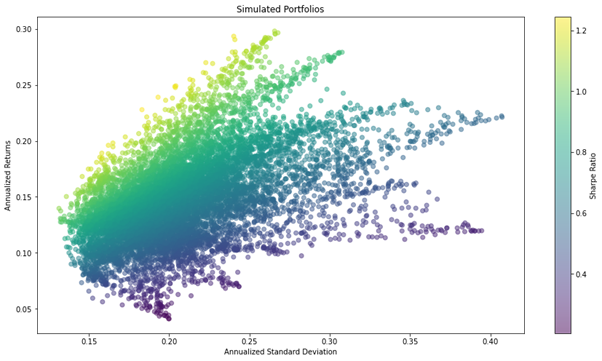
ここからは、理想的なポートフォリオの構成比率を求めます。
効率的フロンティア
ポートフォリオ内の各戦略の週次リターンを入れたデータフレームweekly_returnsから、期待リターンmean_retと共分散行列cov_matrixを計算します。
mean_ret = weekly_returns.mean()
cov_matrix = weekly_returns.cov()
期待リターン、共分散行列を求めたら、任意の重み(ポートフォリオの構成比率)weightsを引数にして、シャープレシオを求める関数を定義できます。
必要に応じてリスクフリーレートrf_rateを指定してください。
あとからscipy.optimize.minimizeで重みを最適化できるように、符号を反転したシャープレシオを戻り値とします。
def neg_sharpe_ratio(weights, mean_ret, cov_matrix, rf_rate=0):
r = (weights @ mean_ret + 1) ** periods_per_year - 1
sd = np.sqrt(weights @ cov_matrix @ weights * periods_per_year)
return -(r - rf_rate) / sd
neg_sharpe_ratioを目的関数としてscipy.optimize.minimizeを利用し、シャープレシオが最大となる重みを求めることができます。
先ほどの乱数を使って生成したシミュレーション上に、最大シャープレシオを表示します。
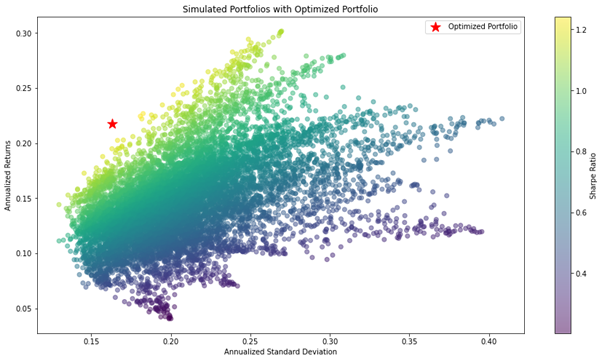
求めたポートフォリオは、インサンプル内で乱数で生成したどのポートフォリオよりも、シャープレシオの値が優れたものとなります。
最大シャープレシオと同様に、最小リスクポートフォリオの構成比率も求めることができます。
任意の重みweightsのポートフォリオのリスク(年率換算した標準偏差)を求める関数portfolio_stdを定義します。
def portfolio_std(weights, mean_ret, cov_matrix):
return np.sqrt(weights @ cov_matrix @ weights * periods_per_year)
portfolio_stdを目的関数として重みweightsを最適化することで、インサンプル内の最小リスクの構成比率を求めます。
ここでリターン(年率換算した平均値)の範囲を制限し、範囲内で最適化を行うことで、任意の目標リターンの中でインサンプル内のリスクが最小となる構成比率を求めることが可能です。
以下は目標リターンの範囲を反復し、効率的フロンティア(Efficient Frontier)を求めプロットしています。
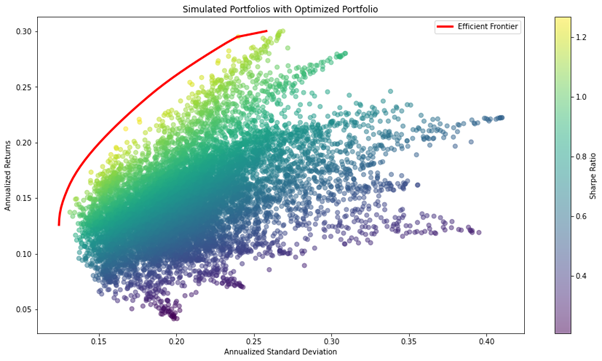
効率的フロンティアによって、インサンプル内の最適なポートフォリオの構成比率を計算することが可能です。
平均分散アプローチの注意点と課題点
ここまで説明した、効率的フロンティアによって検出できるポートフォリオの構成比率はインサンプルの最適ポートフォリオなので、算出した最適ポートフォリオは、アウトオブサンプルで評価する必要があります。
『ファイナンス機械学習』16章によると、相関構造は長期的には安定しないため、とくに投資対象が高い相関をもって分散のニーズが高まるほど、アウトオブサンプルで不安定なものとなると指摘されています。
このグラフは、最大シャープレシオとなるポートフォリオを、算出期間をずらしながら計算した構成比率を示しています。

計算した期間によっては、一つの戦略に大きな比重がかかっていることがわかります。
このアプローチは、計算期間に優秀だったアセットに大きな重みを与えてしまうため、フォワード期間の傾向の変化に対して、不安定になる可能性があります。
階層的リスクパリティ
ポートフォリオを少数のアセットに集中させずに、ポートフォリオ全体でリスクを分散するために、階層的リスクパリティを考察します。
階層的リスクパリティは、ポートフォリオ内にあるリターンの傾向が類似したアセットを、階層的クラスタリングを用いてグループ化した後に、リスクを分散させるための比率を決定するアプローチです。
『ファイナンス機械学習』 16章を参考に、階層的リスクパリティの仕組みを3つの段階、①ツリークラスタリング②準対角化③再帰的二分に分けて解説します。
ツリークラスタリング
ポートフォリオの週次リターンや月次リターンの相関行列を作成し、距離行列に変換します。
距離行列の各列同士のユークリッド距離を計算して、新たな行列とします。
ここでは各列同士の距離を計算しているため、特定ペアの相関ではなく、相関行列全体を使って導かれています。
ユークリッド距離が最も近いペアをクラスターとして、クラスターができれば次はクラスターと他のアセットとのペア、あるいはクラスターとクラスターのペアをまた新たなクラスターとし繰り返すことで、最終的に階層構造のクラスタリングを実現します。
scipy linkageを利用することで、階層的クラスタリングは簡単に実行できます。
これはポートフォリオの週次リターンweekly_returnsから相関行列、距離行列を作成してscipy linkageによる階層的クラスタリングを実行するコードです。
import numpy as np
import pandas as pd
from scipy.cluster.hierarchy import linkage, dendrogram
corr = weekly_returns.corr() # 相関行列
dist = np.sqrt((1 - corr) / 2) # 距離行列
# 階層的クラスタリング
link = linkage(dist, 'single')
dendro = dendrogram(link)
このグラフは、階層的クラスタリング結果のデンドログラムに各数値を表示させたものです。
数値は距離行列の各列のユークリッド距離を示しており、それぞれがどれくらい類似しているかを階層構造にしています。

以下は、scipy linkageによる階層的クラスタリングの結果を、デンドログラム上に描画するコードです。
plt.figure(figsize=(15, 4))
dendro = dendrogram(link)
for i, d, c in zip(dendro['icoord'], dendro['dcoord'], dendro['color_list']):
x = 0.5 * sum(i[1:3])
y = d[1]
plt.plot(x, y, 'o', c=c)
plt.annotate(f"{y:.4f}", (x, y), xytext=(0, -8),
textcoords='offset points',
va='top', ha='center')
plt.ylim(bottom=0)
plt.show()
こちらは、距離行列の各列のユークリッド距離行列を作成するコードです。
# 距離行列のユークリッド距離
num_rows = dist.shape[0]
edist = np.zeros((num_rows, num_rows))
for i in range(num_rows):
for j in range(num_rows):
edist[i, j] = np.linalg.norm(dist.iloc[i] - dist.iloc[j])
pd.DataFrame(edist, index=corr.index, columns=corr.columns)
階層的クラスタリングの結果と比較することで、ユークリッド距離を基にクラスタリングしていることが確認できます。
準対角化
次に、階層的クラスタリングの結果を基に、ポートフォリオ内の順番を並び替えます。
階層的クラスタリングの結果は、ユークリッド距離が近い組み合せは隣り合わせとなり、遠い組み合せは対角上に並んでいることになります。
scipy dendrogramの戻り値のキー’leaves’に、クラスタリング後のソートされた順番が格納されています。
dendro = dendrogram(link)
sorted_tickers = corr.index[dendro['leaves']].tolist()
左は並び替え前の相関ヒートマップ、右は並び替え後の相関ヒートマップです。
並び替えたことにより、ヒートマップがグラデーションとなっているのは相関が高いもの同士が隣り合っている様子を表していることになります。

再帰的二分
最後に、並び替えを行った後の共分散行列を用いて、ポートフォリオの構成比率(重み)を割り当てていきます。
並び替え後のポートフォリオを2分割し、分散が大きいほどポートフォリオの比重を小さくするようにリスクを調整しています。
2分割と分散の逆数に基づいた重み付けを、トップダウン方式で全てのアセットに割り当て終えるまで繰り返します。
以下は、再帰的二分を実行するためのコードです。
# 指定したアセットの分散の逆数を求める
def get_cluster_var(cov, cluster_items):
cov_ = cov.loc[cluster_items, cluster_items]
w_ = (1 / np.diag(cov_)) / (1 / np.diag(cov_)).sum()
return (w_ @ cov_ @ w_).item()
# 共分散行列
cov = weekly_returns.cov()
weights = pd.Series(1, index=sorted_tickers)
clusters = [sorted_tickers]
while len(clusters) > 0:
# アセットを2分割
clusters = [c[start:stop] for c in clusters
for start, stop in ((0, int(len(c) / 2)),
(int(len(c) / 2), len(c)))
if len(c) > 1]
# 重みの割りあて
for i in range(0, len(clusters), 2):
cluster0 = clusters[i]
cluster1 = clusters[i + 1]
cluster0_var = get_cluster_var(cov, cluster0)
cluster1_var = get_cluster_var(cov, cluster1)
weight_scaler = 1 - cluster0_var / (cluster0_var + cluster1_var)
weights[cluster0] *= weight_scaler
weights[cluster1] *= 1 - weight_scaler
グラフは、ポートフォリオの構成比率を、二分割ずつ割り当てる様子を監視したものです。

このように、ポートフォリオの構成比率を決定するアプローチを、階層的リスクパリティと呼びます。
平均分散と階層的リスクパリティの比較
上4つの円グラフは、平均分散アプローチによって最適ポートフォリオを求めた結果の構成比率を示します。
下4つの円グラフは、階層的リスクパリティによって求めた構成比率を示します。

結果を見比べると、平均分散によるポートフォリオは一つのアセットに非常に大きな比率が割り当てられるのに比べ、階層的リスクパリティは偏った構成比率にはなっていません。
さらに、構成比率を注意深く見てみると、平均分散によるポートフォリオは計算する期間によって比率が大きく変化していますが、階層的リスクパリティによるポートフォリオは比率が大きく割り当てられるアセットが安定していることがわかります。
構成比率が計算する期間によって大きくは変化せず、構成比率が大きく偏ることもない階層的リスクパリティは、平均分散よりもアウトオブサンプルで安定した結果を期待でき、先に挙げた課題点をクリアしていると考えられます。
参考書籍 『ファイナンス機械学習 ―金融市場分析を変える機械学習アルゴリズムの理論と実践』(マルコス・ロペス・デ・プラド著、金融財政事情研究会 2019/12/6) 『Machine Learning for Algorithmic Trading: Predictive models to extract signals from market and alternative data for systematic trading strategies with Python, 2nd Edition』(Stefan Jansen著、 Packt Publishing Limited 2nd版 2020/7/31)
本記事の執筆者:藍崎@システムトレーダー
| 本記事の執筆者:藍崎@システムトレーダー | 経歴 |
|---|---|
 |
個人投資家としてEA開発&システムトレード。 トレードに活かすためのデータサイエンス / 統計学 / 数理ファイナンス / 客観的なデータに基づくテクニカル分析 / 機械学習 / MQL5 / Python |
EA(自動売買)を学びたい方へオススメコンテンツ

OANDAではEA(自動売買)を稼働するプラットフォームMT4/MT5の基本的な使い方について、画像や動画付きで詳しく解説しています。MT4/MT5のインストールからEAの設定方法までを詳しく解説しているので、初心者の方でもスムーズにEA運用を始めることが可能です。またOANDAの口座をお持ちであれば、独自開発したオリジナルインジケーターを無料で利用することもできます。EA運用をお考えであれば、ぜひ口座開設をご検討ください。
本ホームページに掲載されている事項は、投資判断の参考となる情報の提供を目的としたものであり、投資の勧誘を目的としたものではありません。投資方針、投資タイミング等は、ご自身の責任において判断してください。本サービスの情報に基づいて行った取引のいかなる損失についても、当社は一切の責を負いかねますのでご了承ください。また、当社は、当該情報の正確性および完全性を保証または約束するものでなく、今後、予告なしに内容を変更または廃止する場合があります。なお、当該情報の欠落・誤謬等につきましてもその責を負いかねますのでご了承ください。