「オプティマルf」を用いた資金管理方法｜ケリー基準（公式）についても解説

---

トレードで長期的なリターンをプラスにさせるためには、期待値がプラスである可能性が高いシステムを選ぶことと、短期的に発生するドローダウンに耐える資金管理が必要です。
この記事では、プラスの期待値を持つシステムで効率的なリターンを得るための資金管理について解説します。

複利効果とドローダウンの回復

グラフはロット数を固定した単利運用(青)と、口座残高とロット数の比率を固定した複利運用(橙)を比較したものです。

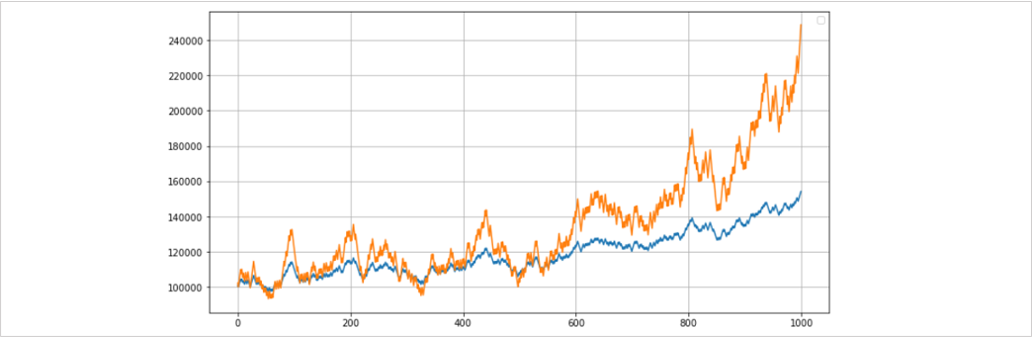
口座残高とロット数の比率を固定した複利運用は、口座残高が高くなるほどロット数が上がっていくため利益も損失も大きくなっていき、システムにプラスの期待値があれば長期では幾何的なリターンを得ることが理論上は可能です。

このような複利効果を発揮するためには、無理のない比率で運用する必要があります。

このグラフはロット数を固定して運用したときの単利損益グラフ(青)と、同じシステムでリスクを過剰にとった固定比率の複利損益グラフ(橙)の比較です。

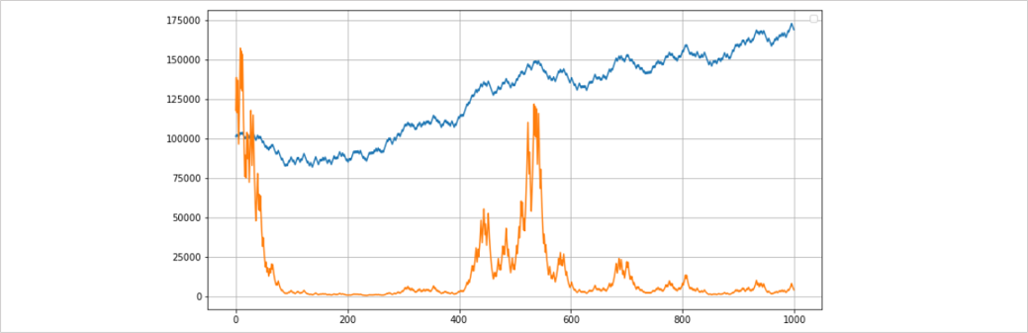
本来ならプラスの期待値があるシステムですが、過剰な資金管理では最終的なリターンがマイナスになってしまっています。

固定比率による複利運用において、発生した損失率と、それを回復させるために必要なリターン率は数値が一致しません。
残高10万円のときに20%のドローダウンがあれば8万円となりますが、8万円を10万円にするには25%のリターンが必要です。

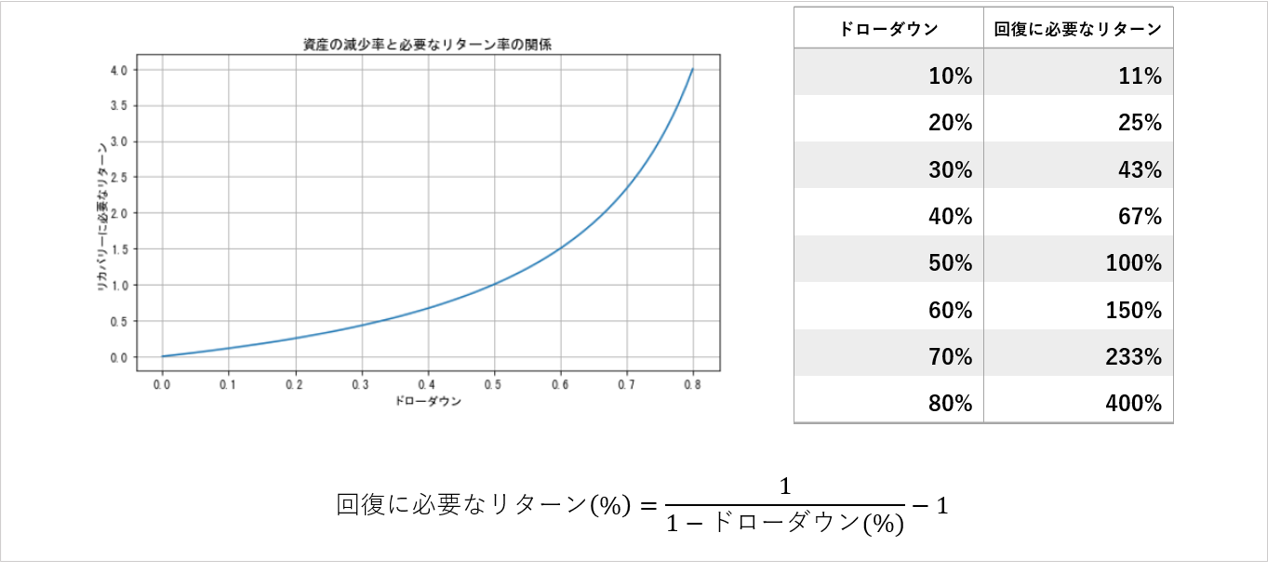
発生したドローダウンが大きいほど、回復に必要なリターン率が大きくなってリカバリーが困難になります。

回復に必要な期間にも違いがあります。

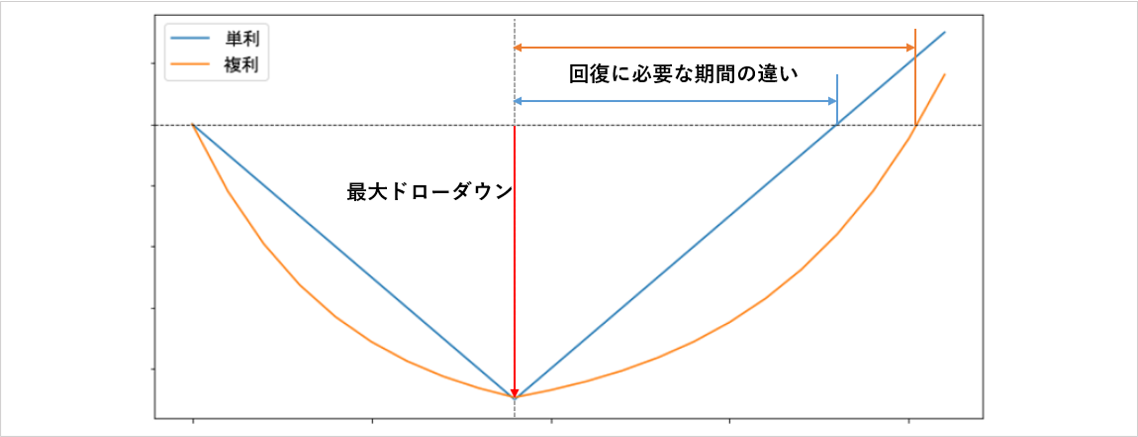
単利でプラスの期待値があるシステムも過剰な比率で複利運用すると最終的なリターンがマイナスになるのは、途中のドローダウンが大きくなりすぎて回復が困難になっているからです。

ケリー基準

単利でプラスの期待値があるシステムが複利効果を得ると最終的なリターンは大きくなりますが、リスクを過剰に取るとドローダウンを回復できなくなるため逆に最終的なリターンは小さくなっていくことを、ここまでで解説しました。

ケリー基準(Kelly criterion)は、最終的なリターンを最大化するための複利運用比率を求めます。

利益と損失の比率bと勝率pからリターンを最大化するための比率fの関係はこのようになります。

p=51%、b=1.1となるように乱数を生成して、単利リターン(青)をケリーの公式を適応した複利リターン(橙)をグラフにします。

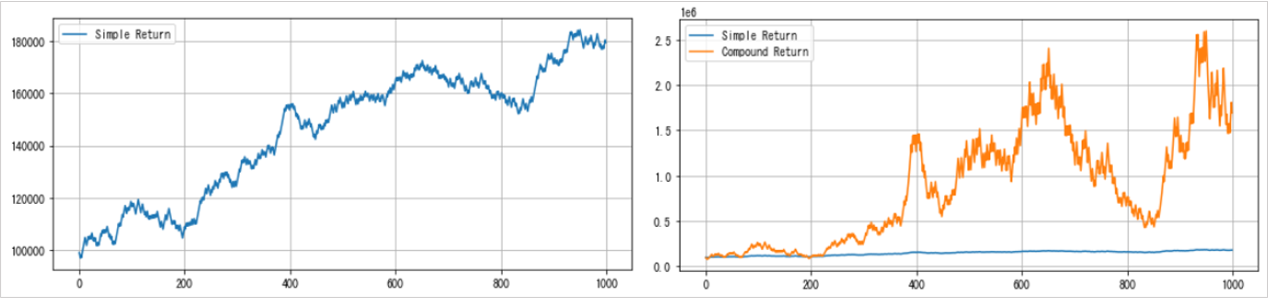
複利効果により大きなリターンとなることがわかります。

上記したケリーの公式では、勝率pと利益と損失の比率bが既知であることと、利益の金額と損失の金額が常に同額であることが前提となっています。
そのため、この式を直接トレードの資金管理に当てはめることは望ましくありません。

トレードシステムのオプティマルfの求め方

リターンが最大となる固定比率fをオプティマルfといいます。
実際のトレード損益は、利益の金額と損失の金額が常に同額にはならないため、ケリーの公式では正確なオプティマルfを求めることができません。

「ラルフ・ビンスの資金管理大全 / ラルフ・ビンス(著)」(パンローリング)では、この問題を解決するために次の式を提案しています。

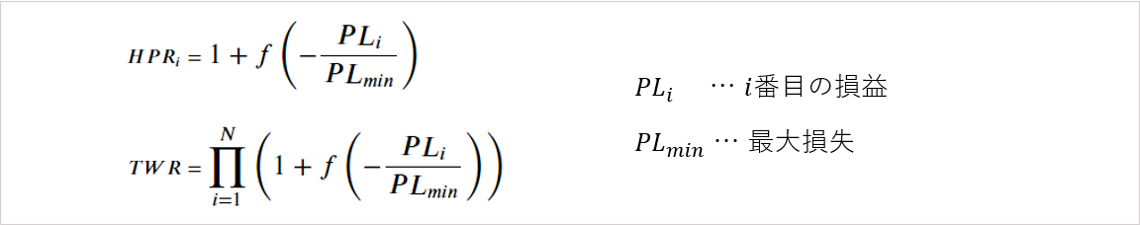
トレード損益データに対してHPRをそれぞれ求め、求めたHPRを総乗してTWRを計算します。
fの値は0から1までの範囲で可変させ、TWRが最大になるfがオプティマルfとなります。

トレード損益に対してHPRの計算式を当てはめて、f=0.01、 f=0.02、 f=0.03…と変化させた結果を表にしています。

HPRの計算結果の表を列ごとに総乗すると、f=0.01、 f=0.02、 f=0.03…と変化させたときのTWRが求まります。
このグラフはfの値を0から0.01ずつ上げて1まで101通りのTWRを計算した結果です。

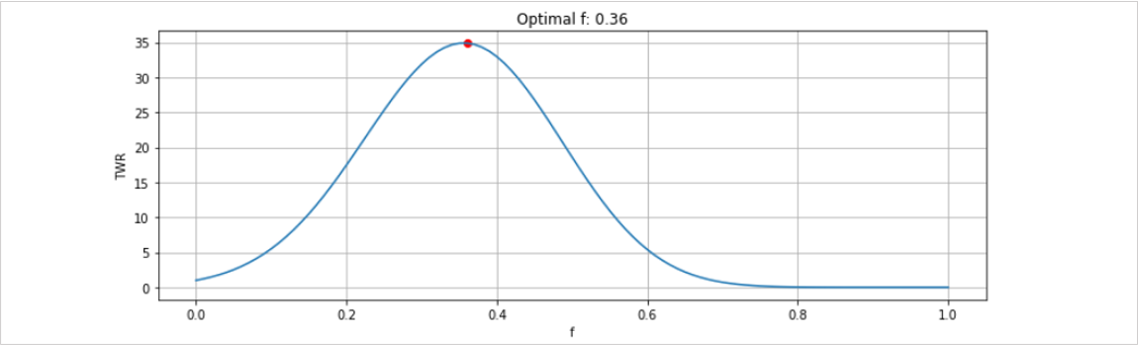
グラフの頂点は f = 0.36 となりました。
つまりこの例では、オプティマルf = 0.36 となります。

元のトレード損益が1ロットであるなら、

• ロット数 = 口座残高 × f ÷ 最大損失

という計算でロット数を決めることでリターンを最大化できます。
今回の例では、fに0.36を代入します。

オプティマルfによる複利運用のシミュレーションです。

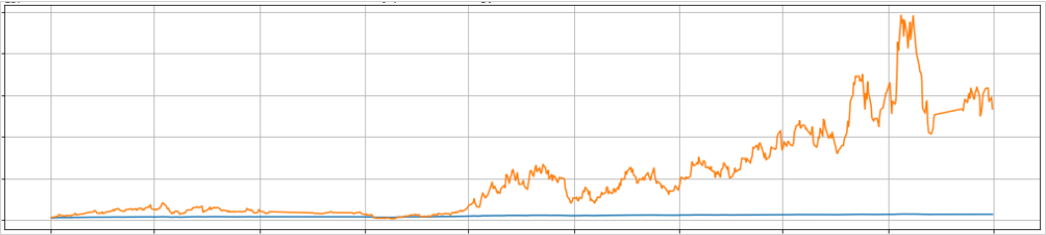
ただし、これは既知の損益結果に対して後からオプティマルfを計算しているので、現実的な検証結果ではありません。
フォワード期間のオプティマルfは、計算結果のオプティマルfと異なるので、その不確実性を考慮して余裕を持った値にする必要があります。

最大損失が重要な理由

HPRの計算式は分母が最大損失、分子が各損失にfをかけたものになっています。
この最大損失は標本内の最大損失ですので、損益の中の一つと値が一致します。

• ● f=1のときは次の1トレードが最大損失だった場合、口座残高がちょうど全損するように調整させています。
• ● f＝0.5で次の1トレードが最大損失だった場合、それまでの損益に関わらず口座残高の50%の損失となります。
• ● f＝0.1で次の1トレードが最大損失だった場合、それまでの損益に関わらず口座残高の10%の損失となります。

不確実性が高い損益において「最大ドローダウンを許容範囲に収める。」というアプローチは、ロット数を固定しない固定比率の資金管理ではとくに困難になります。
fを使った固定比率では、最大ドローダウンではなく最大損失が重要なものと捉えて、どんなときでも常に次の1トレードの損失額を任意の水準に収めるようなアプローチになります。

フォワード期間でのオプティマルfの利用

バックテストでの損益でオプティマルfを計算しても、それがフォワード期間のオプティマルfと一致することはほとんどありません。

次のグラフのようなバックテスト結果を例に考えていきます。
これは10年分のバックテスト結果を1年ごとに区切って、10個のグラフに表示しています。

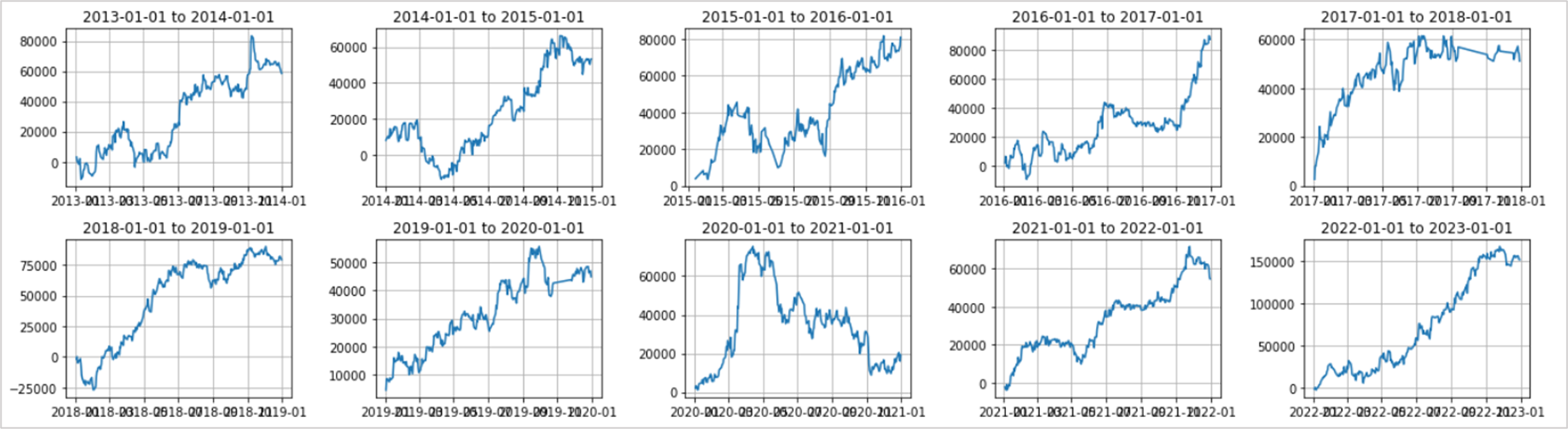
このグラフのそれぞれの期間に対してオプティマルfを計算していきます。

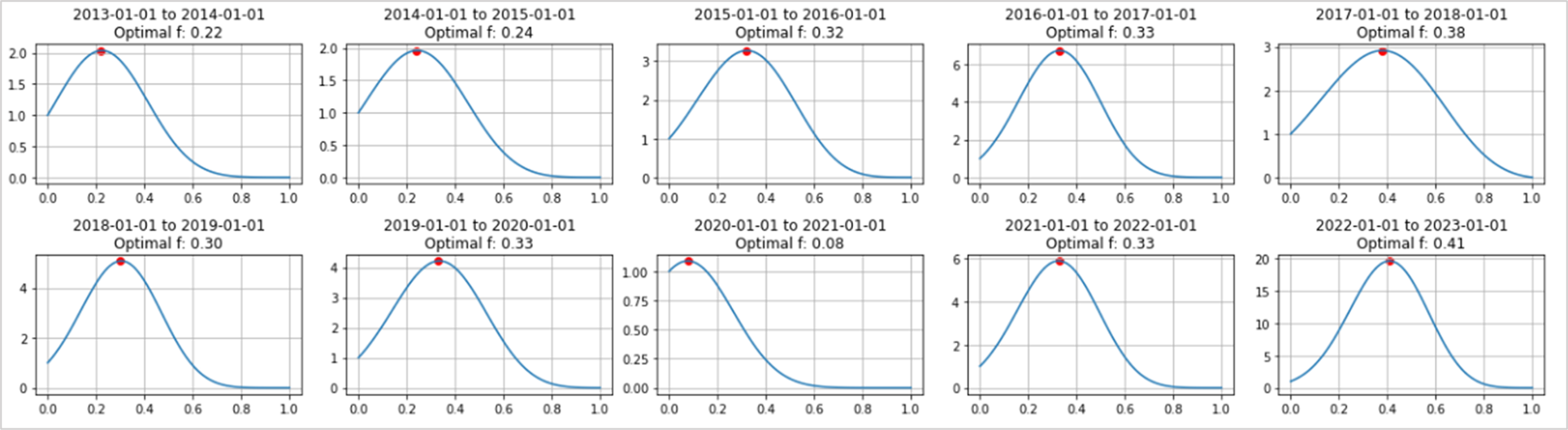
この例では、2020-01-01から2021-01-01までの期間が不調だったのでオプティマルfは0.08と低い値となっています。
2020年以前はオプティマルfがだいたい0.3くらいだったことを考えると、それをそのまま当てはめて実運用していれば、大きすぎるリスクを取ることになっていたことになります。

オプティマルfというものは、すでに確定した結果から後付けで最適固定比率を求めるものであることに注意しなければいけません。
やみくもに、バックテストで計算したオプティマルfをフォワード期間に当てはめるのではなく、フォワード期間で成績が大きく下振れするかもしれないと想定したうえで、fの値を決める必要があります。

モンテカルロ法を用いたオプティマルfの想定

下は先ほどの10年分のバックテスト結果を1年ごとに区切ったバックテスト例を、通常通り10年通してグラフ化したものです。
右側には損益のヒストグラムを表示しています。

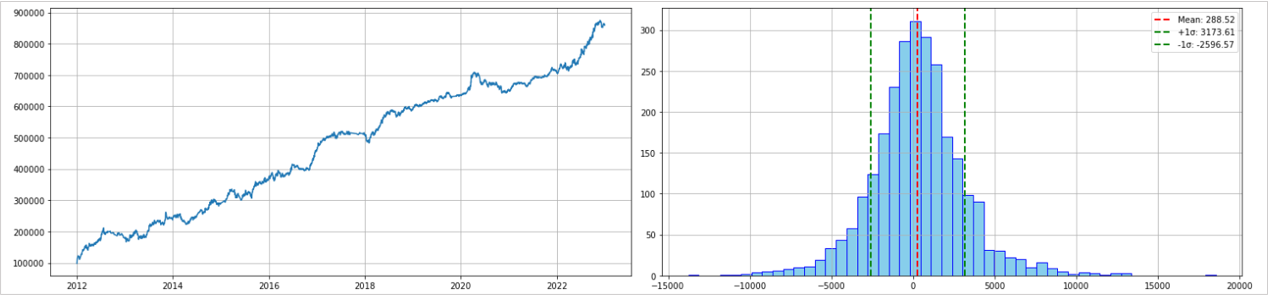
損益が独立試行または独立試行として扱っても問題ないとするなら、このヒストグラムと同一の確率分布からサンプリングすることで、フォワード期間で起こり得る損益の想定ができると考えられます。
つまり、フォワード期間の損益がバックテストと同じ確率分布に従うと仮定しています。

バックテストの取引回数(サンプルサイズ)が十分に大きいとき、最も簡単なモンテカルロシミュレーションは、バックテスト結果から重複をゆるして任意の数をランダムサンプリングし、新たな標本を生成することです。
この方法は、バックテストと同一の確率分布からサンプリングすることを目的として、バックテストにないシミュレーションを行います。

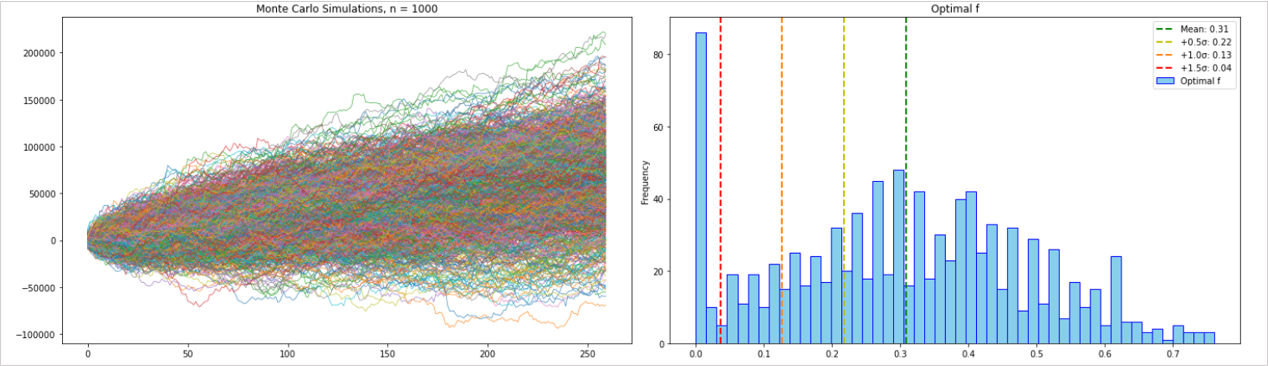
モンテカルロシミュレーションを1000回行った結果と、それによって得られたオプティマルfの分布です。

• ● 平均: 0.31
• ● -0.5σ: 0.22
• ● -1.0σ: 0.13
• ● -1.5σ: 0.04

という結果になっています。

オプティマルfが低い結果は、シミュレーションで下振れしたものになります。
多少フォワード期間の結果が下振れしてもリスク過多にならないようにと考えるなら、平均よりも低い-1.0〜-1.5σ辺りを採用するほうが安全と言えます。

-1.0〜-1.5σという基準は、分布の大部分をカバーしたいという狙いであるため、必ずしもこれである必要はありません。
他の例でいうと、平均の半分、3分の1…などでも同様の効果が期待できるはずです。

スタートトレード分析を用いたオプティマルf振れ幅の想定

モンテカルロシミュレーションは、損益が独立試行であると仮定して行われます。
しかし、トレード戦略の中には独立試行として扱うと分析精度が悪化する、従属性の強い戦略もあります。

このような場合は、モンテカルロシミュレーションの代わりにスタートトレード分析(Rolling window)を用いることにします。

スタートトレード分析は、バックテスト損益から任意の回数分ずつ抽出開始位置をずらしながらサンプリングする分析方法です。
テクニカル指標の移動平均線と同じ計算の要領と考えてください。

パフォーマンスの評価としてスタートトレード分析でシャープレシオを評価する方法は、とくによく用いられており、Rolling Sharpe Ratioとして知られています。

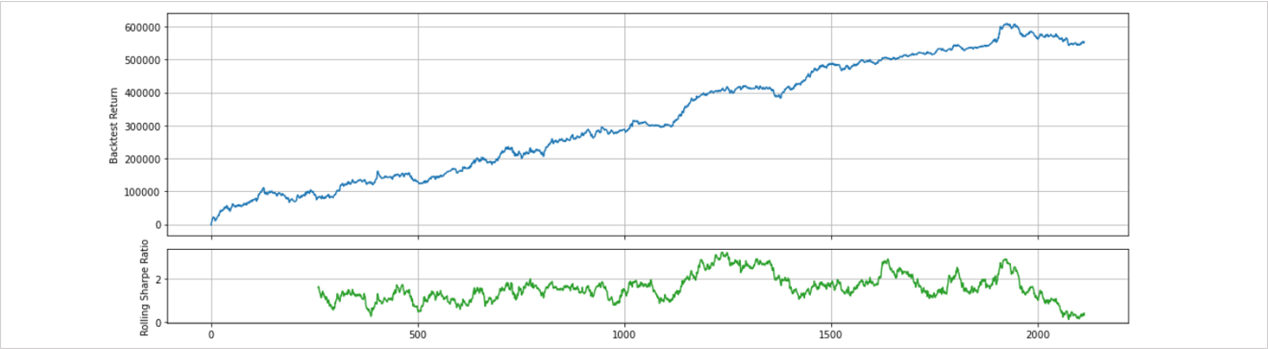
上のグラフがバックテスト結果で下がRolling Sharpe Ratioです。

次はこれをオプティマルfに置き換えてRolling Optimal fにします。

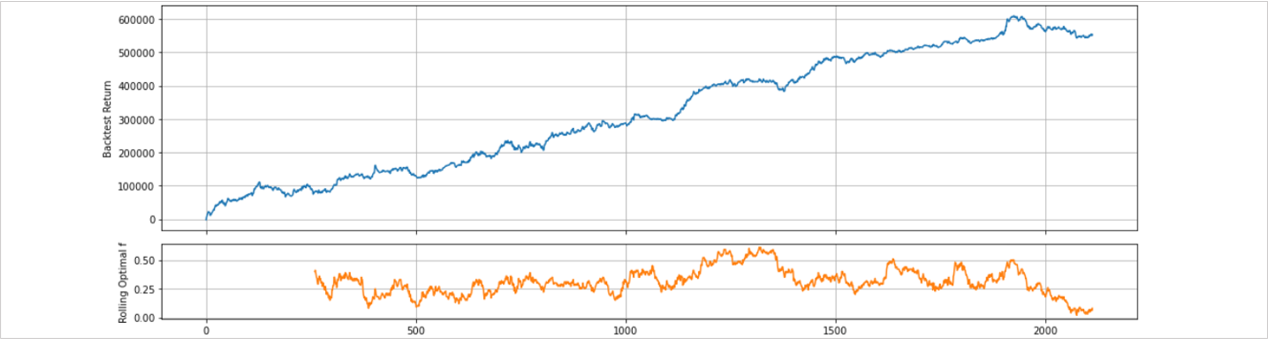
オプティマルfは最適固定比率を示すものですが、単利リターンが安定したものほど大きなリスクと取ることが可能となるため、シャープレシオと相関関係になります。

モンテカルロシミュレーションと同様にオプティマルfをヒストグラムにします。

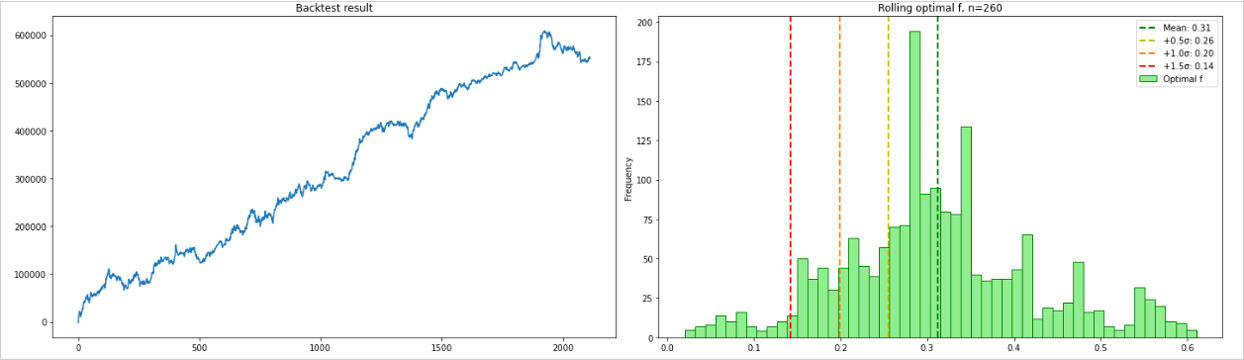
今回の例ではスタートトレード分析の方がモンテカルロシミュレーションよりも楽観的な結果となっています。

今回使用したバックテストデータは独立試行に近いものだったため、モンテカルロシミュレーションの方が、より厳しい基準となったのだと考えられます。

結果の解釈はモンテカルロシミュレーションと同じです。
多少フォワード期間の結果が下振れしてもリスク過多にならないようにと考えるなら、分布の大部分をカバーできるように-1.0〜-1.5σ辺りを採用するほうが安全と言えます。

シャープレシオが低いシステムのオプティマルf

これはバックテストのドローダウンが大きく不安定な損益だったシステムに対してオプティマルfの想定を行ったものです。

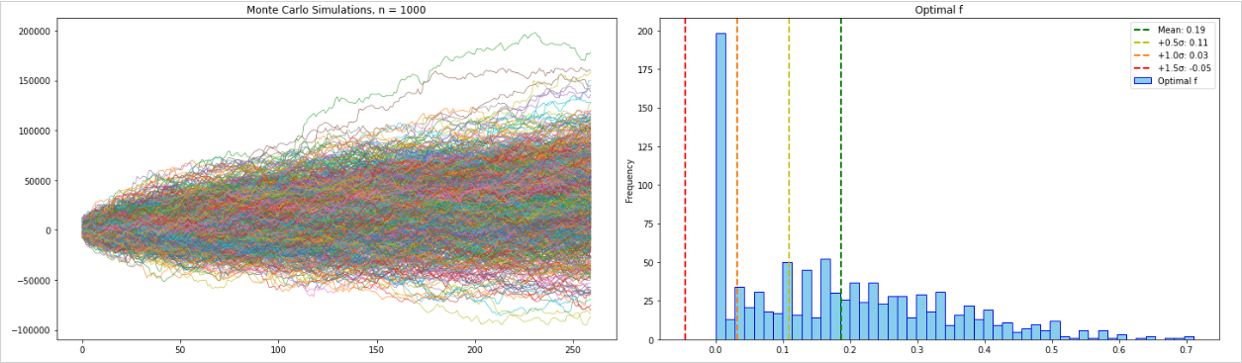
モンテカルロシミュレーションによるオプティマルf

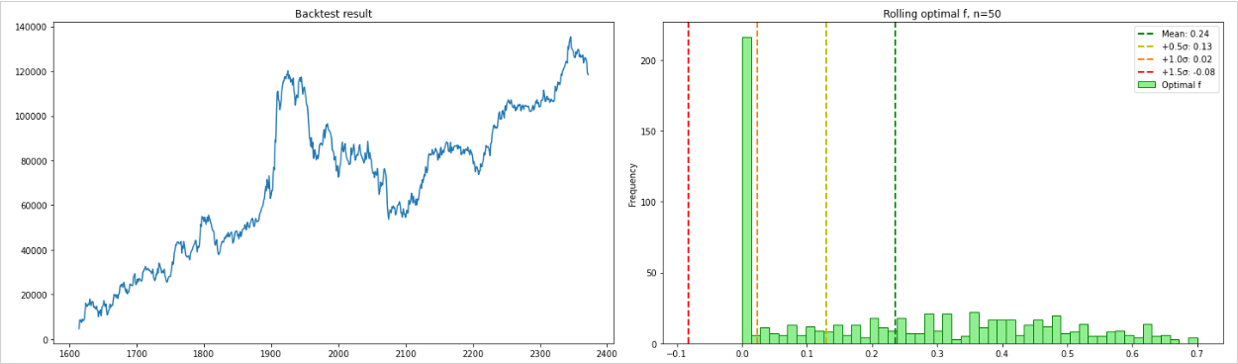
スタートトレード分析によるオプティマルf

オプティマルfは最適固定比率を示すものであるため、0より低くはなりません。
オプティマルfが0になる確率が高いシステムは最適固定比率が0、つまり「取引しない」が最適であることを示しています。

このように見方を変えれば、最適固定比率オプティマルfはシステムの評価指標にもなり得る可能性があります。

この記事では、「リスク過多にならないように。」を強調しましたが、実際のトレードでは一つの取引口座に運用資金の何％を入金しているか、どのような出金ルールにしているかなどによっても、取れるリスクの大きさは異なります。
記事の内容を鵜吞みにせず、自身の環境や口座管理に合わせたポジションサイジングを考えることが大切です。

---

本ホームページに掲載されている事項は、投資判断の参考となる情報の提供を目的としたものであり、投資の勧誘を目的としたものではありません。投資方針、投資タイミング等は、ご自身の責任において判断してください。本サービスの情報に基づいて行った取引のいかなる損失についても、当社は一切の責を負いかねますのでご了承ください。また、当社は、当該情報の正確性および完全性を保証または約束するものでなく、今後、予告なしに内容を変更または廃止する場合があります。なお、当該情報の欠落・誤謬等につきましてもその責を負いかねますのでご了承ください。

---