平均回帰戦略とは？共和分ADF検定を用いたトレード戦略について解説

---

平均回帰戦略は定量的なトレードにもよく利用される戦略の一種です。
もし価格変動にランダムウォークではない平均回帰性を見つけることができれば、買われすぎで売り、売られすぎで買うことで、優位性のあるトレードを行うことができます。
この記事では、平均回帰戦略としての統計的裁定取引(Statistical Arbitrage：StatArb)と、平均回帰性を数学的に発生するための、共和分法について解説します。

統計的裁定取引

平均回帰戦略のひとつに統計的裁定取引があります。
よくある統計的裁定取引に、2つの銘柄を組み合わせ相対価格に基づいて売買判断を行うようなものがあります。
つまり、買われすぎ売られすぎは絶対的な判断はせずに、他の銘柄に対して買われすぎなのか、売られすぎなのかを判断します。

裁定取引とありますが無リスクで利益を出す裁定取引とは違って、短期的には利益が出るか損失が出るかわからない、試行回数を重ねて長期的にプラスに収束させていくような通常のトレード戦略のひとつです。

統計的裁定取引の一例を解説します。
組み合わせる2つの銘柄は、高い相関関係であることが理想的です。
2つの相関がある銘柄の価格差(スプレッド)に平均回帰性があるとき、統計的裁定取引の機会が発生します。
価格差に平均回帰性があるとき、スプレッドが一時的に広がったときにそれが元に戻る(平均に回帰する)という動きを狙ってロングショートします。

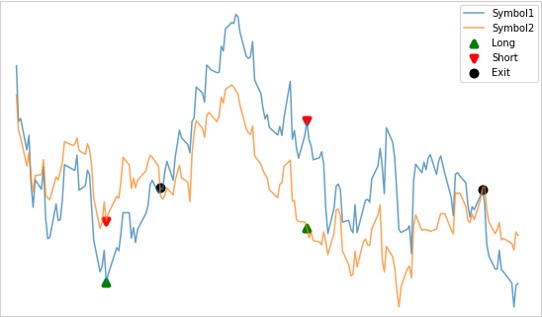
他の銘柄に対して買われすぎなのか、売られすぎなのかを判断するため、片方の銘柄がペアの銘柄の過大・過小評価を反映している関係性を、経済的な視点でも説明できると精度が高くなると考えられます。

平均回帰性とは

時系列データに平均回帰性がある状態がどのようなものか、ランダムウォークと平均回帰を比較して確認します。

ランダムウォークの例

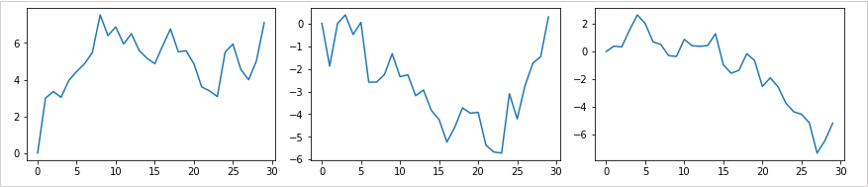
平均回帰の例

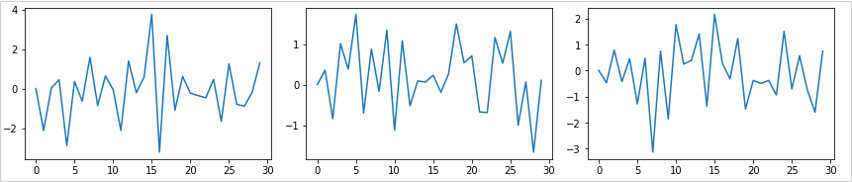
ランダムウォークは1つ前のデータにランダムなデータを足していくような時系列データとなり、平均回帰は時系列の中心に軸があり、その近くをバラツキながら進むデータです。
ランダムウォークは価格の決定は過去のデータに依存していない状態です。

平均や分散も変化しない時系列の特性を定常性といいます。
この定常性、もしくは定常性を持つ確率過程を示す定常過程は、時系列解析を行う上で重要な概念です。

定常過程がどんなものか知るために、ラグ1の自己回帰過程(AR(1)過程)が定常である状況を確認します。
AR(1)過程とは「1つ前のデータに依存した時系列の確率過程」のことで、現在レートと1つ前のレートに何かしらの関係性がある時系列データを意味しています。

AR(1)過程は上記の式で表されます。
ホワイトノイズは時系列データのランダム成分です。
ここではわかりやすいように定数項は常に0として考えます。

左からφ = -0.5、φ = 0.0、φ = 0.5、φ=1.0と変化させたグラフです。
φ = -0.5のときが最も上下に細かく振れていて、右のグラフになるにつれて振れは穏やかに推移します。
φ = 1.0のとき、1つ前のデータにランダムなデータを足していくような時系列データとなり、この条件はランダムウォークと同じで、平均に回帰しません。
このようなφの絶対値が1.0より低い時系列データを定常過程と呼び、φ = 1.0となる時系列データを単位根過程と呼びます。
定常過程となるということは、平均値に回帰する特性があることを示しています。

平均回帰戦略が成立するかどうかの判定は、時系列が定常過程であるかを調べることがひとつの手段です。

時系列データが定常かどうかを調べる手段の一つに拡張ディッキーフラー検定(ADF検定)があります。

ADF検定とは帰無仮説が「時系列に単位根がある」となる検定です。
この帰無仮説が棄却されるということは、その時系列はランダムウォークではない確率が高いことを示します。

ADF検定をPythonのstatsmodelsライブラリーを用いて行う例を紹介します。

```
import yfinance as yf
from statsmodels.tsa.stattools import adfuller

# USD/JPYのデータを取得
pair = 'JPY=X'
data = yf.download(pair, start='2022-04-01', end='2022-09-01')
usd_jpy_data = data['Close']

# ADF検定
adf_test_result = adfuller(usd_jpy_data)

# 結果を表示
print('ADF Statistic:', adf_test_result[0])
print('p-value:', adf_test_result[1])
print('Critical Values:')
for key, value in adf_test_result[4].items():
print('\t%s: %.3f' % (key, value)) 
``` 

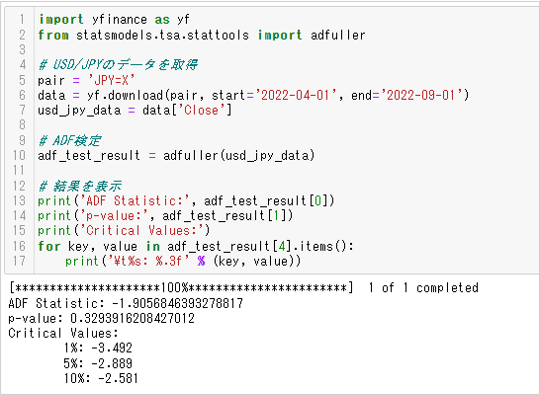
出力しているデータは上から次の通りです。

• 1．検定統計量
• 2．p値
• 3．検定統計量の棄却限界値(1%、5%、10%)

単純にp値(p-value)が0.05未満だと帰無仮説を棄却できるとすると、結果は「時系列に単位根がある」という帰無仮説を棄却できない、つまりランダムウォークに従うことを否定できないものです。

共和分によるペアトレード

実際には単一の銘柄で平均回帰性を見つけることは困難です。
そこで、2つの銘柄の差に平均回帰性が現れるかを検証します。

相関関係にある2つの銘柄間スプレッドに平均回帰性が現れるなら、ロングショートの組み合わせで利益にすることが可能です。

このような取引機会をもたらすペアを見つけるために利用される統計的な手法に共和分ADF検定(エンゲル・グレンジャーの検定)があります。
共和分ADF検定は、2つの時系列データに対して線形回帰を行い、残差系列の定常性を検定します。
2つの時系列データの線形結合が定常過程であるとき、その線形回帰の残差系列が定常となることを利用しています。

共和分ADF検定をPythonのstatsmodelsライブラリーを用いて行う例を紹介します。

```
import yfinance as yf
import pandas as pd
import statsmodels.tsa.stattools as ts

# 各為替ペアのデータを取得
pairs = ['AUDJPY=X', 'CADJPY=X']
fx_data = {}
for pair in pairs:
data = yf.download(pair, start='2022-01-01', end='2023-01-01')
fx_data[pair] = data['Close']

merged_data = pd.DataFrame(fx_data)

# 欠損値を削除
merged_data.dropna(inplace=True)

# エンゲル・グレンジャー共和分検定
eg_test_result = ts.coint(merged_data['AUDJPY=X'], merged_data['CADJPY=X'])

# 結果を表示
print('T-statistic:', eg_test_result[0])
print('p-value:', eg_test_result[1])
print('Critical Values:')
critical_value_labels = ['1%', '5%', '10%']
for i, value in enumerate(eg_test_result[2]):
print('\t%s: %.3f' % (critical_value_labels[i], value)) 
``` 

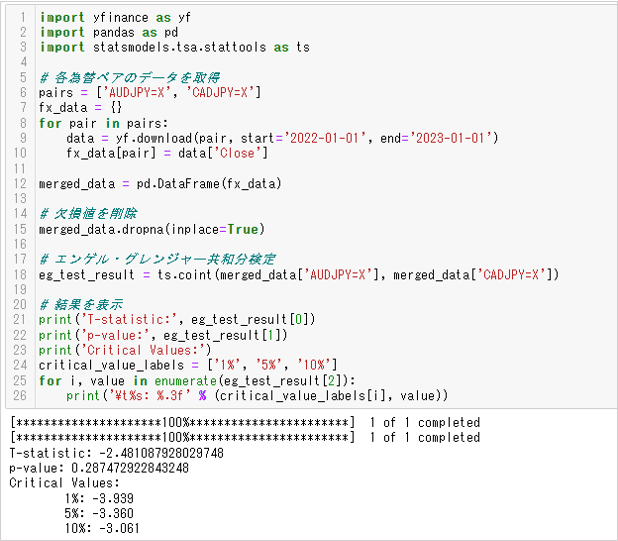
出力しているデータは上から次の通りです。

• 1．検定統計量
• 2．p値()
• 3．臨界値

単純にp値(p-value)が0.05未満だと帰無仮説を棄却できるとすると、結果は共和分の関係ではありません。

このような手順で共和分の関係にあるペアを探し、発見したペアのスプレッドが一時的に広がったときにそれが元に戻る(平均に回帰する)という動きを狙ってロングショートすることで期待値がプラスになることを見込めるトレード(ペアトレード)が可能です。

ロングショートのタイミング

共和分ADF検定によって共和分の関係を検出したペアに対して、平均回帰戦略を仕掛けるときは、単純には「残差の時系列プロット」に平均と標準偏差を示す水平線を引きエントリーのタイミングに利用します。

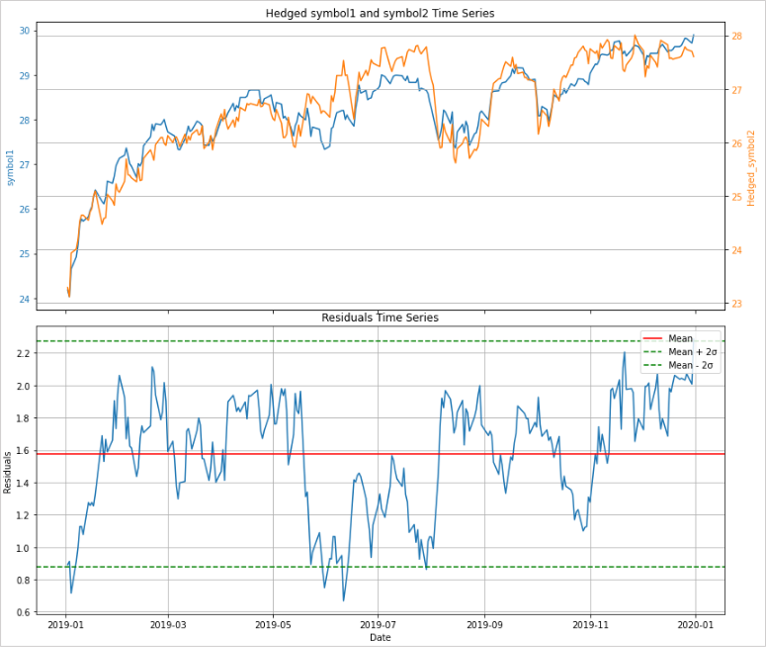
上のグラフは共和分ADF検定によって検出したペア(symbol1とsymbol2)の価格変動を重ねて表示しており、下のグラフはペアを回帰したときの残差の時系列プロットです。

平均値と平均値から±2σに水平線を引いています。
+2σのライン上でsymbol1を売り、同時にsymbol2を買い、そのあと平均値に回帰する価格変動を狙います。

次は売買のタイミングにボリンジャーバンドを利用してみます。

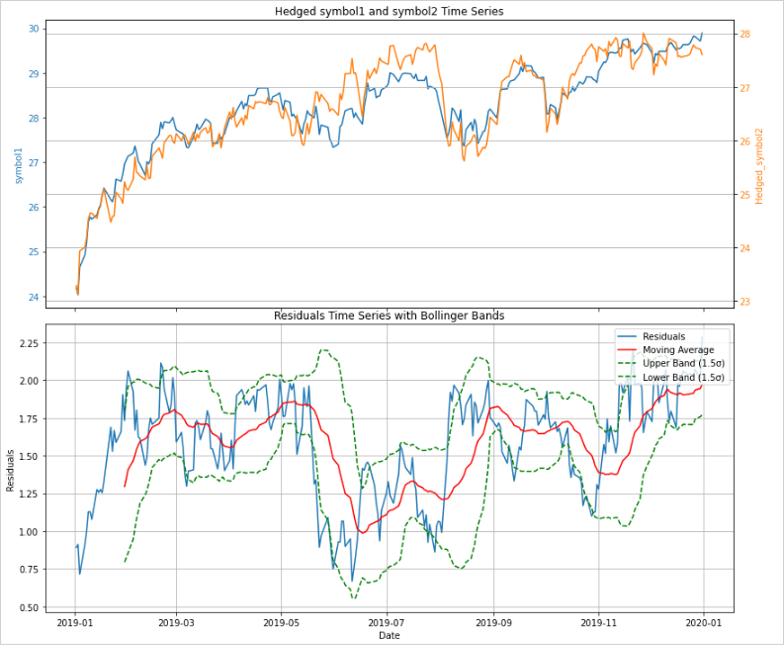
通常のチャートに対してボリンジャーバンドの上下のバンドにタッチすれば逆張りするようなアプローチでは、トレンドの発生で大きな損失を出すリスクがあったり、そもそもランダムウォークでは優位性は生まれません。
共和分の関係にあるペアは残差系列が定常になるため、レンジ相場にボリンジャーバンドの逆張りを当てはめているような状態です。

統計的裁定取引の機会を見つけるために

資源国通貨と一部のコモディティとのペアは、相関関係となることがあります。
この図は、複数の資源国通貨やコモディティに対して、共和分検定のp値を算出しヒートマップに表示したものです。

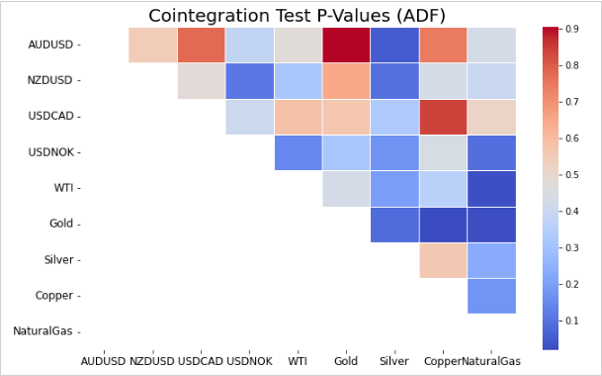
p値は低い方が共和分の関係にある可能性が高いことを示すため、このヒートマップでは濃い青色のペアがそれに該当します。
このようにヒートマップとして表示することで検出を効率化できます。

次のグラフは共和分検定のp値の時間変化を示しています。

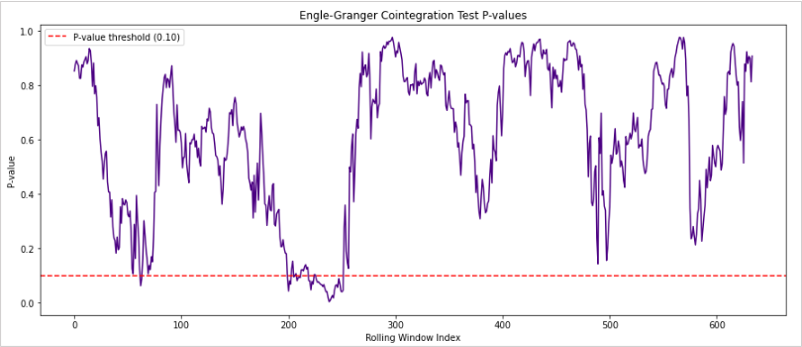
このグラフのデータとして使ったペアは全体で共和分の関係ではないですが、p値が下降するタイミングに周期的なものがあるようにも見えます。
一時的にでも統計的裁定取引の機会が発生し、そのタイミングが予測可能であればトレードに利用できる可能性はあると考えられます。

パフォーマンス評価の注意点

統計的裁定取引に限った話ではないですが、過去のヒストリカルデータで戦略のパフォーマンスを評価するためには、現実的な状況を再現してサンプリングしなければいけません。

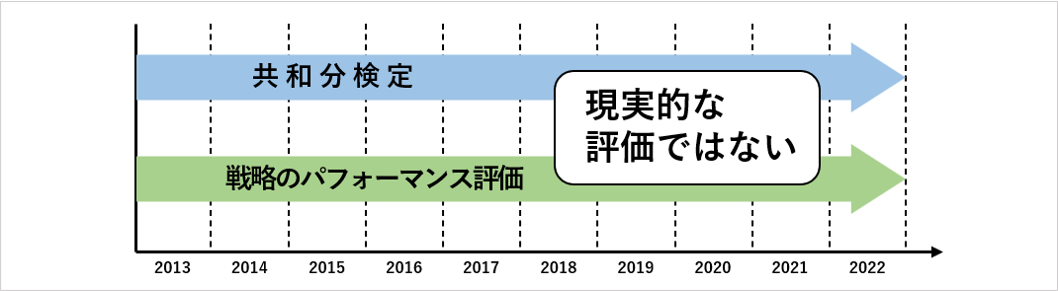
上の図のような戦略のパフォーマンスでは、共和分検定によって「予めこの期間には平均回帰性が存在している」と判明しているところに戦略を当てはめていますが、これは良くない検証です。

これからトレードを開始するような現実的シチュエーションでは、平均回帰性があるかわからない期間に対して「平均回帰性が発生する」という予測のもと、戦略を当てはめる必要があります。

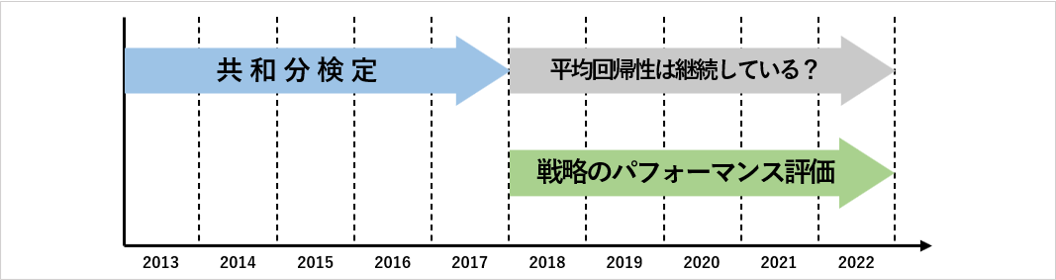
こちらの図では、共和分検定によって平均回帰性が判明したペアに対して「その後の期間も平均回帰性が継続する」という予測のもと、戦略を当てはめているため、現実的な状況を再現したサンプリングができていいます。

統計的裁定取引に関する研究

ペアトレード、統計的裁定取引は1980年代からトレードに利用されており、その後も多くのクオンツや研究者によって発展してきました。
現在は機械学習の手法を取り入れてたものも多くあります。
ここでは、いくつかの文献を紹介します。

Kitapbayev Y. and Leung T. (2017).「Optimal mean-reverting spread trading: nonlinear integral equation approach.」

ポジションのエントリーや決済のタイミングについては様々なアプローチがあります。
この文献では、OU過程(Ornstein-Uhlenbeck process)という平均回帰する確率過程に対して、最適停止問題を適応することで、エントリーや決済のタイミングを測って高いパフォーマンスを出そうという試みをしています。

Beckmann J, Czudaj R, Arora V (2017) 「The Relationship Between Oil Prices And Exchange Rates: Theory And Evidence」

共和分の関係が発生する背景には、対象の銘柄の現在レートが過大評価なのか過小評価なのかをペアとなるもう片方のレートとの相対評価によって説明できているという状況が必要です。
この文献は、原油価格と為替レートの相互にはたらく関係を考察しています。
原油価格と為替レートが上記のような過大・過小評価ができる関係性となっているかのヒントになると考えられます。

Figueira M, and Horta N (2022)「Machine Learning-Based Pairs Trading Strategy with Multivariate」

この文献では、2銘柄以上の多変量ペアのスプレッドから機械学習(ARIMAとXGBoost)を用いて取引機会を検出するアプローチを提案しています。
統計的裁定取引は相対的な価格の評価から予測可能なエッジを見つけるわけですが、必ずしも2銘柄である必要はありません。
また、スプレッドに対して予測可能な周期やパターンがあるならば、必ずしも平均回帰戦略である必要もありません。

多変量ペアについて(ヨハンセン検定)

この記事では、共和分ADF検定(エンゲル・グレンジャーの検定)を用いてきましたが、別の手段としてヨハンセン検定(Johansen test)があります。
エンゲル・グレンジャーの方法は2変数の共和分を調べるものでしたが、ヨハンセンの方法は3変数以上の共和分ベクトルの同時推定と検定が可能です。

以下のPythonコードはヨハンセン検定の例です。

```
import yfinance as yf
import pandas as pd
from statsmodels.tsa.vector_ar.vecm import coint_johansen

# 各為替ペアのデータを取得
pairs = ['AUDJPY=X', 'CADJPY=X', 'NZDJPY=X']
fx_data = {}
for pair in pairs:
data = yf.download(pair, start='2022-01-01', end='2023-01-01')
fx_data[pair] = data['Close']

merged_data = pd.DataFrame(fx_data)

# 欠損値を削除
merged_data.dropna(inplace=True)

# ヨハンセン共和分検定
result = coint_johansen(merged_data, det_order=0, k_ar_diff=1)

# 結果を表示
print("\n\nトレース検定統計量:")
for i, trace_stat in enumerate(result.lr1):
print(f"r = {i}: {trace_stat}")
print("\nトレース検定の臨界値:")
for i, trace_crit in enumerate(result.cvt):
print(f"r = {i}: 1% = {trace_crit[0]}, 5% = {trace_crit[1]}, 10% = {trace_crit[2]}")
print("\n最大固有値検定統計量:")
for i, max_eig_stat in enumerate(result.lr2):
print(f"r = {i}: {max_eig_stat}")
print("\n最大固有値検定の臨界値:")
for i, max_eig_crit in enumerate(result.cvm):
print(f"r = {i}: 1% = {max_eig_crit[0]}, 5% = {max_eig_crit[1]}, 10% = {max_eig_crit[2]}")
``` 

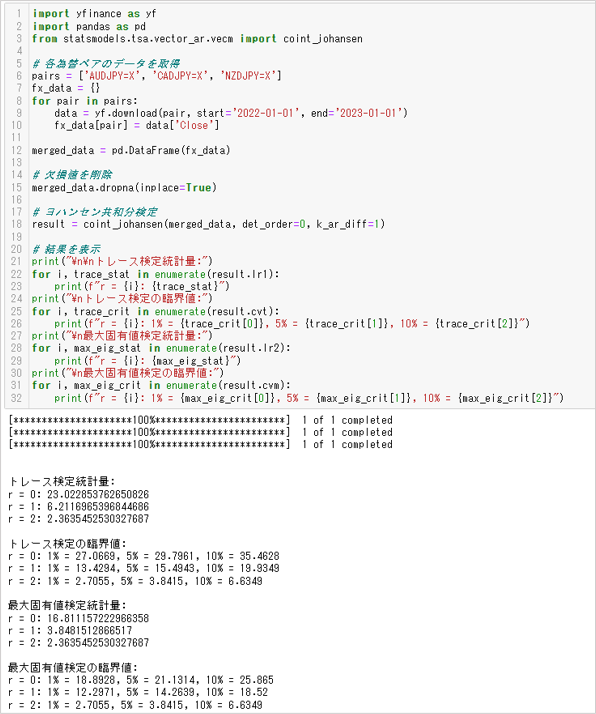
共和分ADF検定は、2変数で回帰を行います。
つまり片方を従属変数、もう片方を説明変数とするのですが、サンプルサイズが小さいときに従属変数と説明変数が入れ替わると結果が変わるという現象が起こります。
また、3変数以上の共和分ベクトルを推定するための体系的な手続きは確立されていません。

ヨハンセン検定は共和分ADF検定の2段階推定(回帰から単位根検定)に頼ることがないため、これらの問題は発生せず、多変量ペアを検証することができます。

3銘柄以上の多変量ペアに相関関係は実際に発生し、そのスプレッドに予測可能な周期やパターン、例えば先行遅行関係などが発生する可能性も十分に考えられます。

本記事の執筆者：藍崎@システムトレーダー

　　　　　 　　　　　　　 　

本記事の執筆者：藍崎@システムトレーダー	経歴
	個人投資家としてEA開発＆システムトレード。 トレードに活かすためのデータサイエンス / 統計学 / 数理ファイナンス / 客観的なデータに基づくテクニカル分析 / 機械学習 / MQL5 / Python

---

本ホームページに掲載されている事項は、投資判断の参考となる情報の提供を目的としたものであり、投資の勧誘を目的としたものではありません。投資方針、投資タイミング等は、ご自身の責任において判断してください。本サービスの情報に基づいて行った取引のいかなる損失についても、当社は一切の責を負いかねますのでご了承ください。また、当社は、当該情報の正確性および完全性を保証または約束するものでなく、今後、予告なしに内容を変更または廃止する場合があります。なお、当該情報の欠落・誤謬等につきましてもその責を負いかねますのでご了承ください。

---