公開鍵暗号とは?仕組みやRSAの計算方法などについて解説
前回のコラムでは送信者と受信者が同じ鍵を持つ秘密鍵暗号方式を前提として換字式暗号について解説しました。
前回記事:暗号技術入門|初歩的な換字式暗号や秘密鍵方式の仕組みを解説
文字を暗号に変換するときに、両者で同じ鍵を持っていれば暗号化に対して復号が正しくできるという原理でした。しかし、秘密鍵暗号は鍵が漏洩すると暗号を第三者に解読されてしまう問題があります。
鍵情報は少なくとも1回は相手方に平文(暗号化されていない文)で送信しなければならないので、それを盗聴されると鍵が漏洩してしまいます。
また、戦争のような状況で暗号表や鍵を載せた船や飛行機が敵の手に渡ると敵に暗号を解読されてしまいます。
この問題を解決する方法として公開鍵暗号方式が発明されて現代ではあらゆる場所で用いられています。
ブロックチェーンの技術においても公開鍵暗号は非常に重要な技術的位置を占めています。
暗号化の鍵を公開しているのに第三者には解読できない不思議さ
公開鍵暗号の使い方を図1に示します。
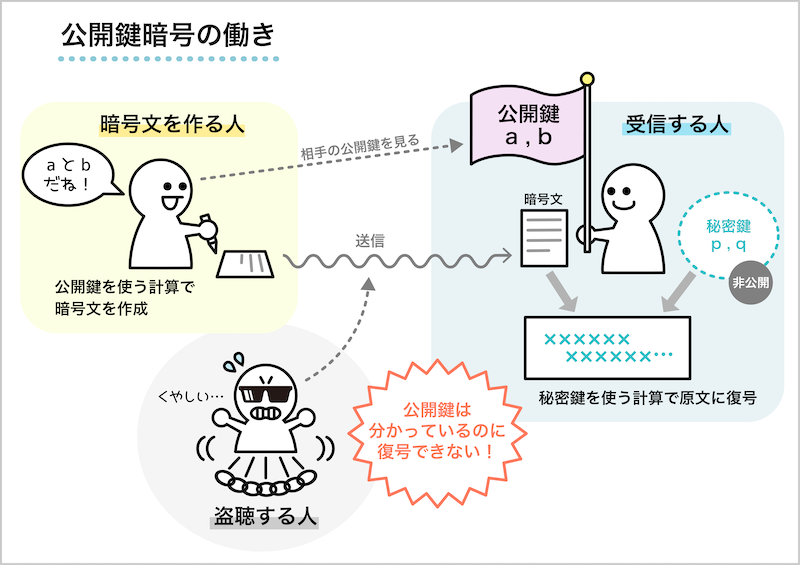
暗号文を受信する人は、自分専用の公開鍵(a,b)と秘密鍵(p,q)を予めコンピュータで計算して準備しておき、公開鍵はホームページなどに公開し秘密鍵は自分だけの情報として秘密にしておきます。
公開鍵と秘密鍵はセットになっていて、公開鍵で暗号化した文はセットになっている秘密鍵を用いないと復号することができません。
暗号文を作って受信者に送りたい人は、受信者が公開している公開鍵(a,b)をコピーしてその鍵を使って暗号文を作り、その暗号文を受信者に送ります。
受信者は自分だけが持っている秘密鍵(p,q)を使って計算することにより復号を実行し暗号文の原文を読むことができるようになります。
暗号化の鍵が分かっているのだから、その鍵を使って暗号化と逆の計算をすれば復号できるのではないでしょうか?
それができれば第三者は簡単に暗号を解読できてしまいますが、なんと、逆向きの計算ができない不思議な計算方法であるRSAというアルゴリズムが発明されたのです。
二つの素数(1とそれ自身でしか除算ができない整数)を掛け算することは簡単ですが、その逆向きの計算で「掛け算した結果の値」を見せられても何と何を掛け算したらその値になるのかが分からない(膨大な計算時間がかかるので事実上計算できない)という原理に基づいています。
このような発明のおかげで解読用の秘密鍵が他人に漏洩する可能性が限りなくゼロにできるようになり、たとえ暗号文が盗聴されたとしても内容を解読される恐れがないのです。
公開鍵暗号「RSA」の計算方法のイメージ
RSA暗号の計算方法はかなり複雑なので、計算方法のイメージを解説しましょう。
(厳密な計算方法については他のホームページの解説を参照していただけばよいと思います。)
RSA暗号では原文の文字コード(整数値)を多数回掛け算して、適当な数値で割った余り(剰余)を暗号に用いる文字コードとします。
図2に原文の文字コードから直接剰余計算をして暗号化するイメージを示します。

文字「A」を意味する整数値65について29で割った剰余を計算すると7になります。
割る数として別の値、例えば41を使うとAの剰余は24になります。
両方について剰余が8になる文字は何かというと、29の剰余では文字「B」を表しますが41の剰余では文字「Z」を表します。
このように剰余を使うと、割られる前の数値が何であるかが一つに定まらなくなってしまうのです。
さて、興味深いことに毎回剰余を計算しながら文字コードの数値を多数回掛け算すると、元の数字に戻ってくるという性質があります。
元の数字に戻る条件は複雑なので他の文献解説に譲りますが、この性質が成立する「ある計算方法」をfと表して暗号計算の流れを図3に示します。
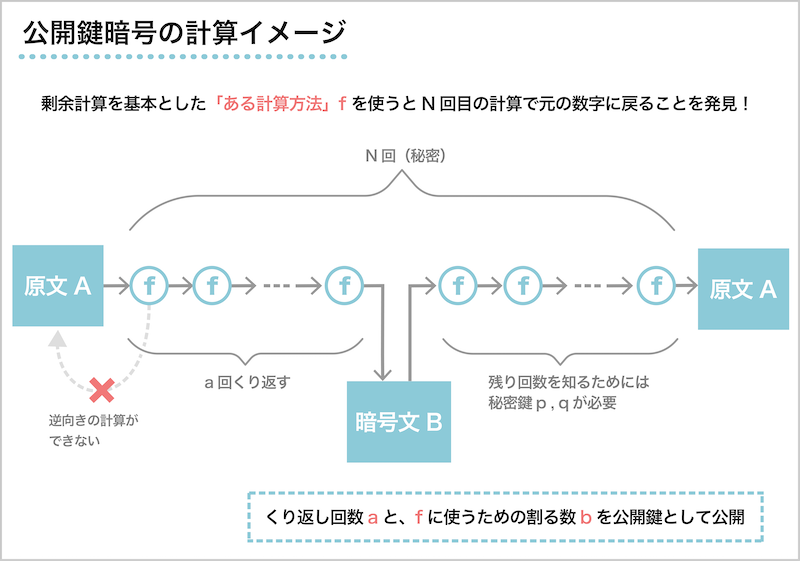
原文Aは計算fをN回繰り返すと原文Aに戻る性質があります。
N回という回数はfの剰余計算をするときに使う値bに依存して決まりますが、bは二つの素数の掛け算になっており、二つの素数が分からない限りN回という回数が計算できません。
二つの素数として非常に大きな値を用いればbから素数を解読することができなくなるのは前述の通りです。
その意味でNは秘密になっています。
公開鍵としては(a,b)の二つの数字を公開しますが、bはfの計算の中で剰余計算に用いる数、aはfを繰り返す回数を示します。
計算fをN回繰り返すと元の文字に戻るのですがa回繰り返した時点ではバラバラの数値になっていて文字として理解できない状態になります。
つまり暗号文Bが完成したことになります。
fの逆向きの計算をすることができないので暗号文Bを解読するためにはfの計算回数が合計N回になるように計算回数を決めなければなりません。
公開鍵を生成するときには同時に秘密鍵(p,q)を生成しますが、そのp,qの値から計算して残り回数を計算することができます。
p,qは暗号受信者しか知らない情報なので第三者には暗号が解読できないのです。
公開鍵暗号方式は最初にRSAが開発されましたが、現在では楕円暗号と呼ばれる方式などもあります。
webのSSHアクセスやICカードに搭載されている電子証明書など、あらゆる場所に利用されています。
Provided by
上野 仁(Hitoshi Ueno)
1984年山梨大学大学院修士課程(計算機科学専攻)修了後、株式会社日立製作所入社。
システム開発研究所、エンタープライズサーバ事業部などで主としてコンピュータアーキテクチャおよび基本ソフトウェアの研究開発に従事。
2015年より第一工科大学東京上野キャンパス情報電子システム工学科教授に就任。
2023年より東京情報デザイン専門職大学教授。
生体信号処理に関するプログラム開発や種々の先端ソフトウェアついての調査研究に興味を持つ。
技術士(情報工学)。
博士(工学)。
ビットコイン(仮想通貨)を学びたい方にオススメのコンテンツ

東京情報デザイン専門職大学教授の上野仁氏監修による暗号通貨・ブロックチェーンの記事一覧です。
本ホームページに掲載されている事項は、投資判断の参考となる情報の提供を目的としたものであり、投資の勧誘を目的としたものではありません。投資方針、投資タイミング等は、ご自身の責任において判断してください。本サービスの情報に基づいて行った取引のいかなる損失についても、当社は一切の責を負いかねますのでご了承ください。また、当社は、当該情報の正確性および完全性を保証または約束するものでなく、今後、予告なしに内容を変更または廃止する場合があります。なお、当該情報の欠落・誤謬等につきましてもその責を負いかねますのでご了承ください。
