線形回帰モデルを使った相場予測の方法を詳しく解説
この記事では、線形回帰を用いた相場予測をするシンプルな実装例を示して、線形回帰を使った予測のイメージを掴んで理解を深めることを目的として解説します。
線形回帰は、機械学習の中でも教師あり学習の回帰に属するモデルです。
数値データを対象にして、観測可能な他の数値データでそれを予測します。
線形回帰がどのように予測するのか
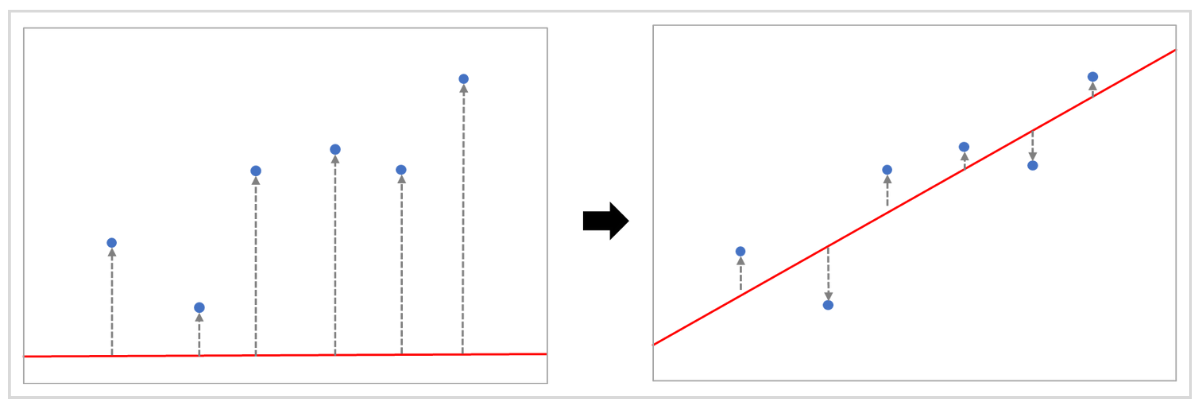
線形回帰のイメージを理解するため、簡単な例を挙げます。
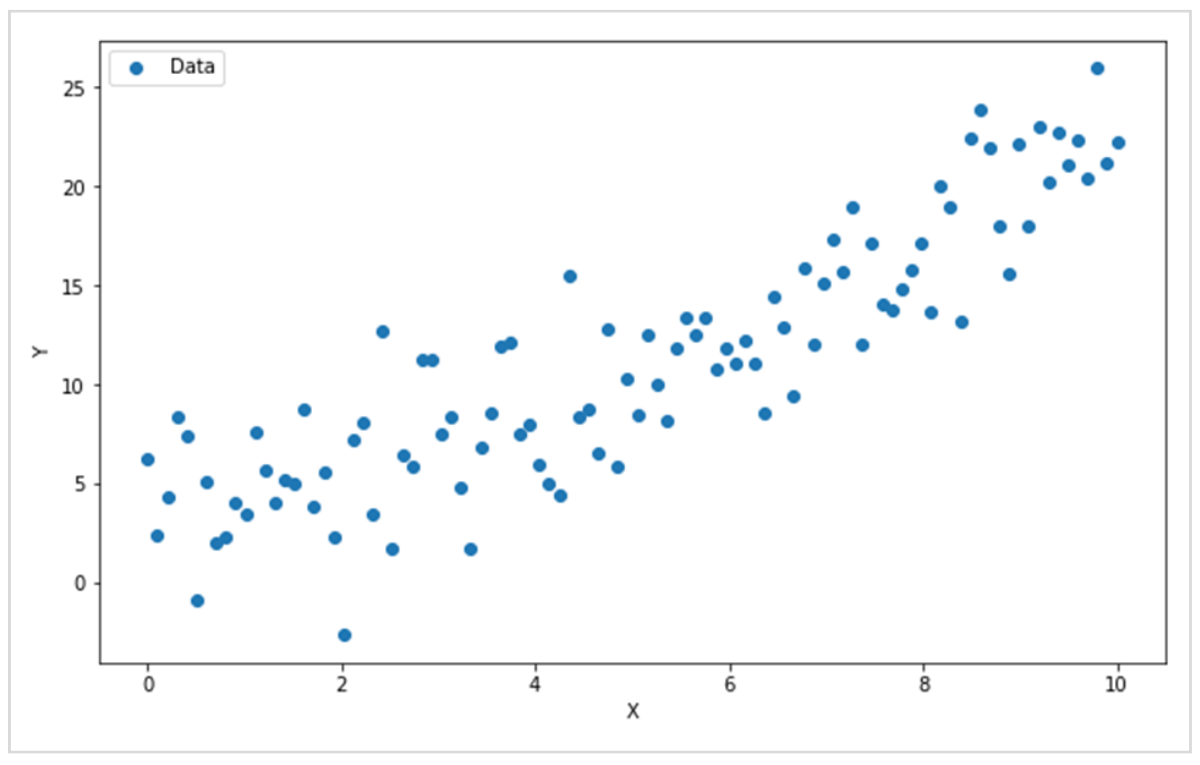
このデータは、XとYにばらつきはあるものの、全体的に右肩上がりの傾向があることが、視覚的にもわかるかと思います。
「Xの値が大きくなるほど、Yの値も大きくなる」という依存関係があるわけです。
このノイズの背景に存在するデータの傾向に、最適化したラインを描画してみます。
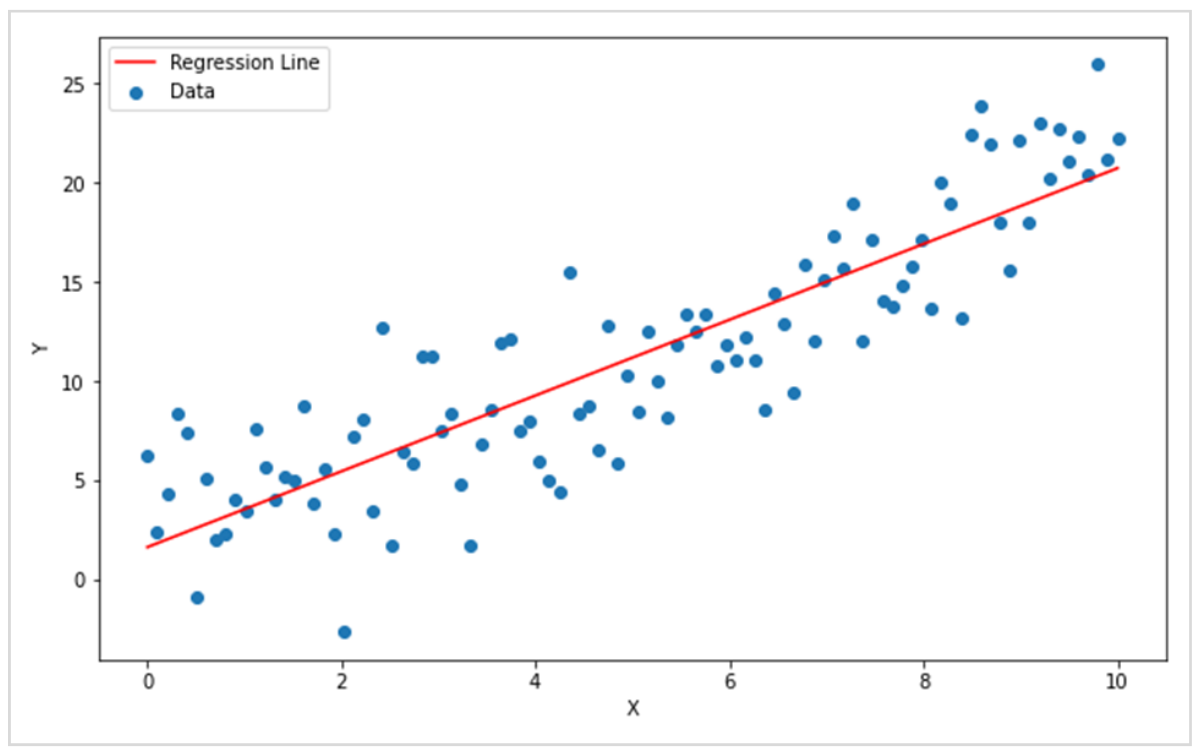
書き加えた赤い直線は、データの傾向にあわせて角度や位置が決まっており、データの傾向を学習した状態といえます。
ここに新しいデータが追加されたとき、Xの値さえわかればYの値は直線との交点をたどって予測できます。
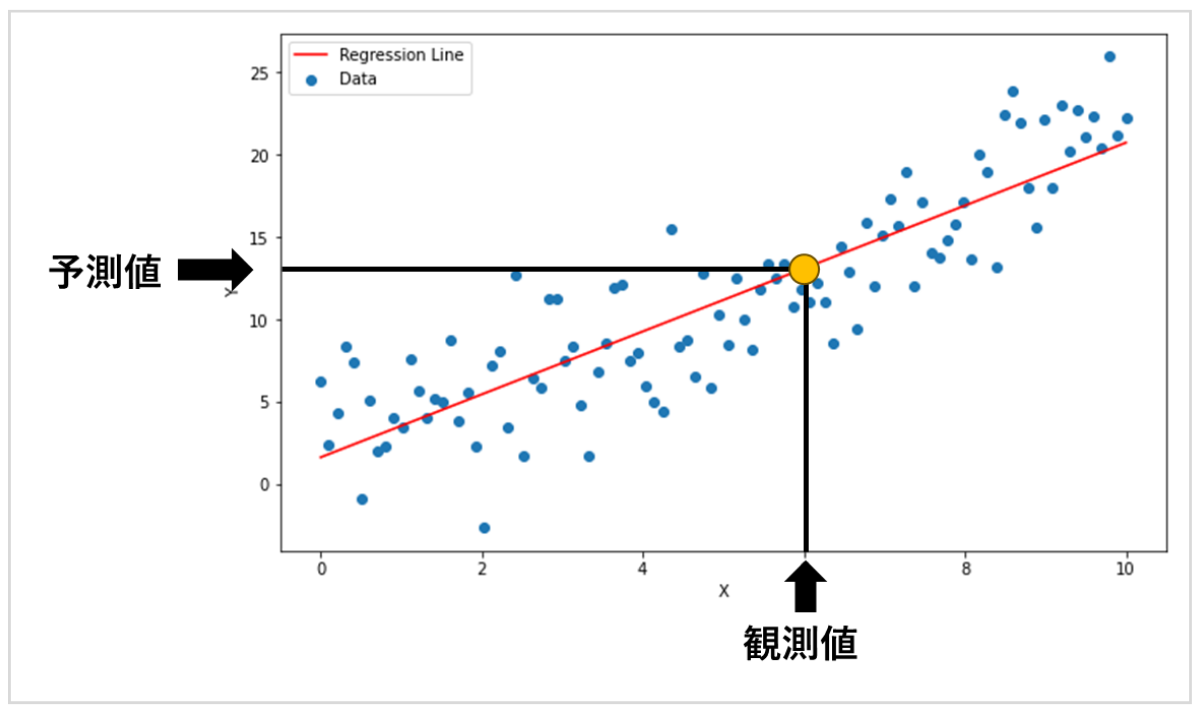
つまり、Yを予測したいデータに、XをYと何かしらの依存関係にある観測可能なデータにすることで、ラインの形状を学習させて予測モデルを作ることが可能です。
例えば、Yを翌日の相場の変動幅、Xを前日まで過去1か月間の変動幅として、仮にこのYとXに確かな依存関係があれば、翌日の相場の変動幅を予測する線形回帰モデルが実現できます。
Yのような予測対象を目的変数、Xのような予測に使う変数を説明変数、YとXは共にデータの特徴を表す数値で特徴量といいます。
実際には、依存関係が明確であるほど予測の精度は高くなるので、簡単に相場を予測できるわけではありません。
しかし、予測対象は相場変動に限らず様々なものに置き換えて考えることが可能なので、アイデア次第で様々な利用方法が生まれます。
線形回帰(OLS回帰)
回帰にもいくつか種類がありますが、よく知られた基本的なものに線形回帰(OLS回帰)があります。
学習用の各データと予測線との距離が最短になるように、予測線のパラメータを最適化するアルゴリズムです。
予測線が直線の場合は、その角度や位置を最適化します。
下のグラフは勾配法を用いて、徐々に実際のデータに対してモデルが学習する様子(予測線を最適化する様子)を可視化したものです。
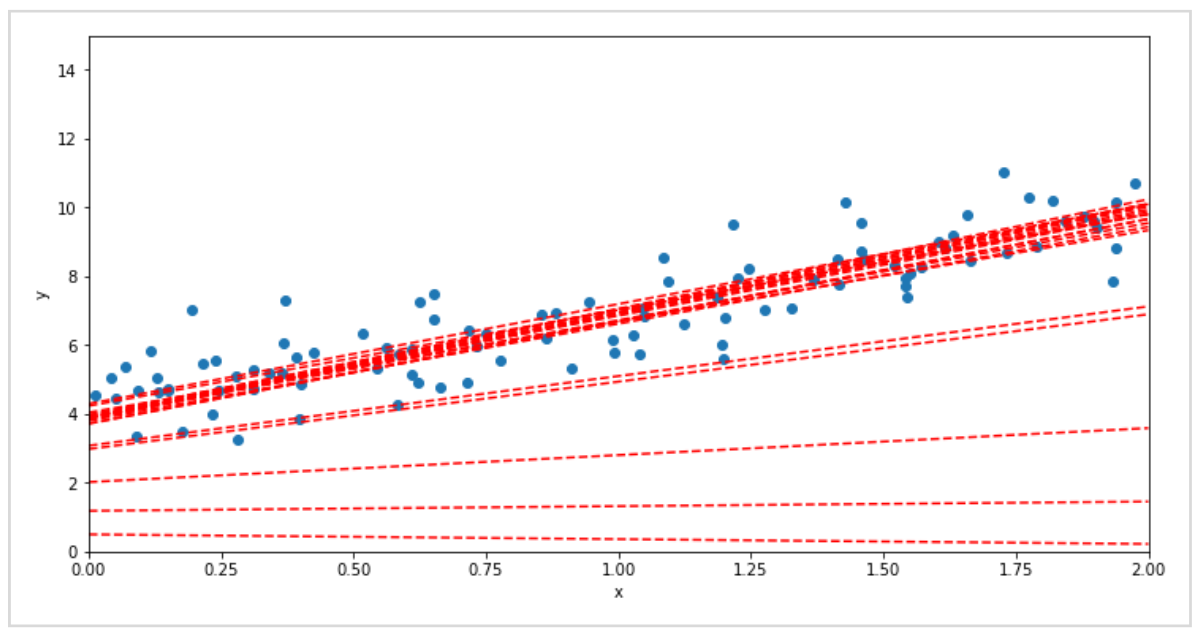
勾配法のようにくり返しの計算によって最適化する方法の他に、方程式を解いて予測線のパラメータを求める方法もあります。
予測線を表す式です。
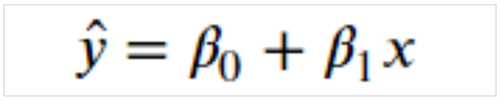
各データと予測線との距離が最短になるaとbは、以下の式で求められます。
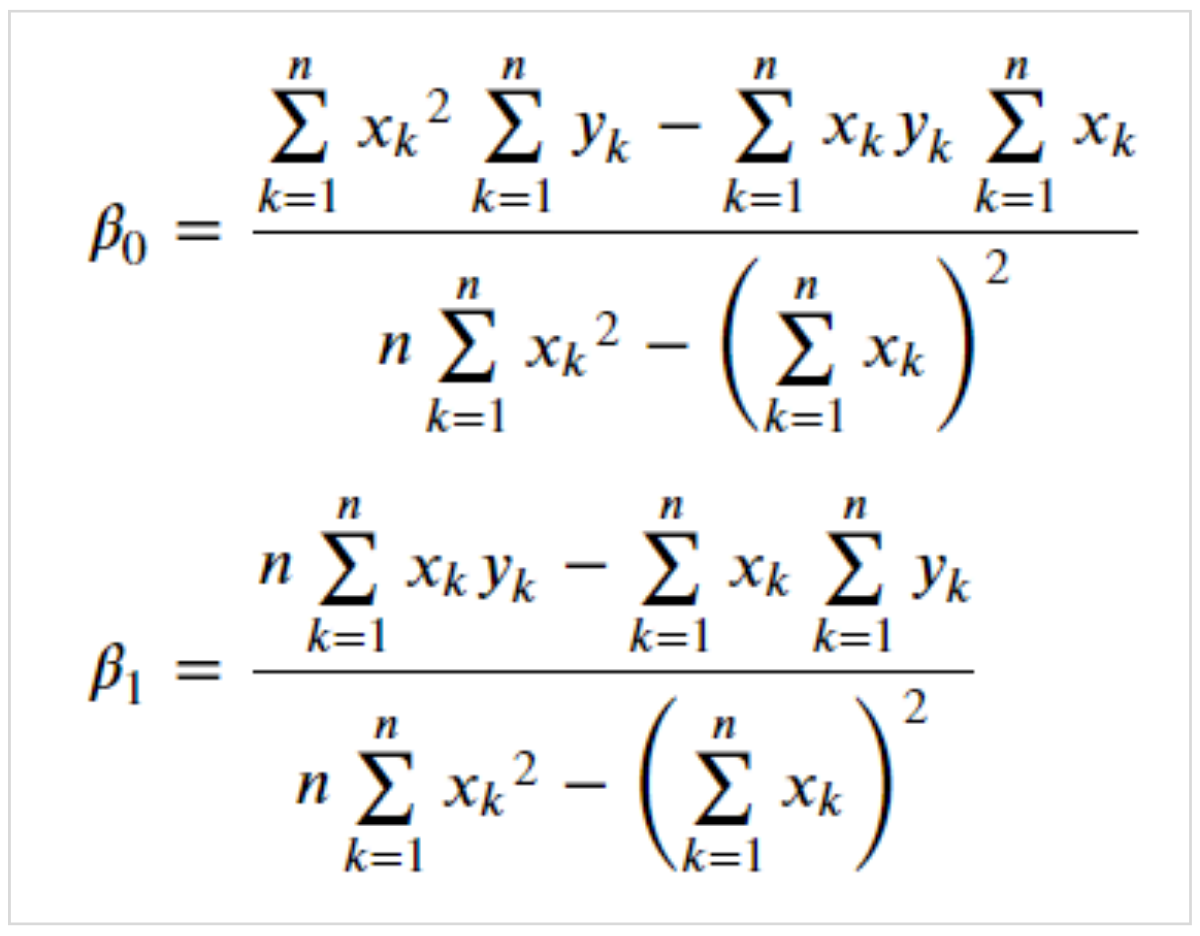
線形回帰モデルは、Pythonのscikit-learnを使用すると簡単に実装できます。
以下は、乱数を用いてサンプルデータを生成し、そのサンプルデータに対して学習するコードです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# サンプルデータを生成
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 線形回帰モデルを学習
lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_predict = lin_reg.predict(X)
# データと予測線をプロット
plt.scatter(X, y)
plt.plot(X, y_predict, c='r')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.title('Linear Regression')
plt.show()
EURとGBPを例にして、線形回帰を実際のデータに使用します。
EURとGBPは共に欧州通貨で、USDに対する価格には相関関係があると知られています。
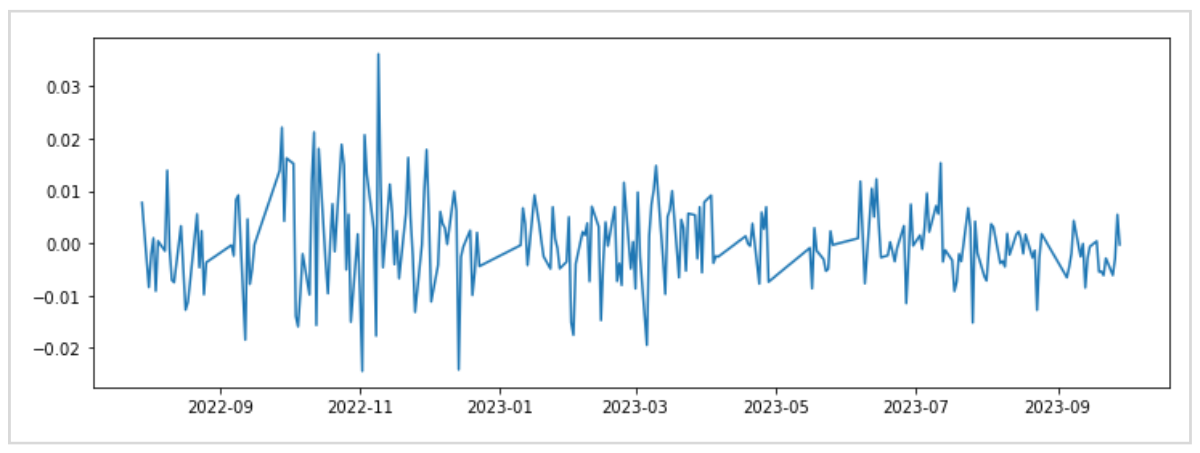
左のグラフはEURUSDとGBPUSDを重ねて表示したもので、右のグラフは日々の対数収益率の分析に予測線を描画したものです。
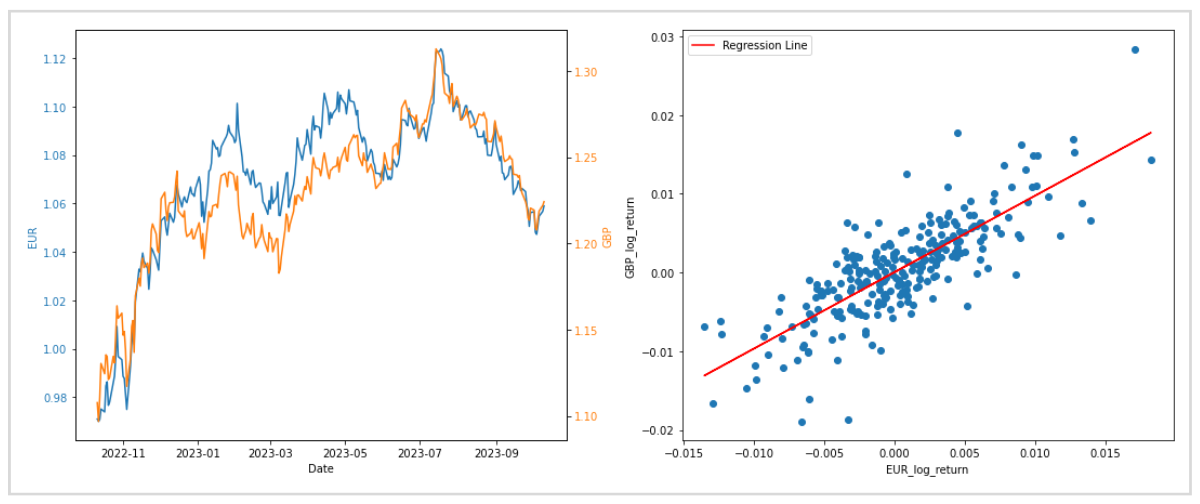
日々の対数収益率の分析から、全体的に右肩上がりの傾向があり、線形回帰による予測がうまく当てはまっていることがわかります。
つまり、EURの対数収益率から同時刻のGBPがどれくらい動いたかを予測することが可能かもしれないことです。
同時刻のレートの予測をしてもあまり恩恵がないので、次は未来のレートを予測対象にしてみます。
線形回帰を用いたシンプルな予測
今回は線形回帰の使用例として、非常にシンプルな仕組みで実践してみます。
予測に必要な特徴量の候補を、OANDA MT5から取得可能なFX、CFDを使って用意します。
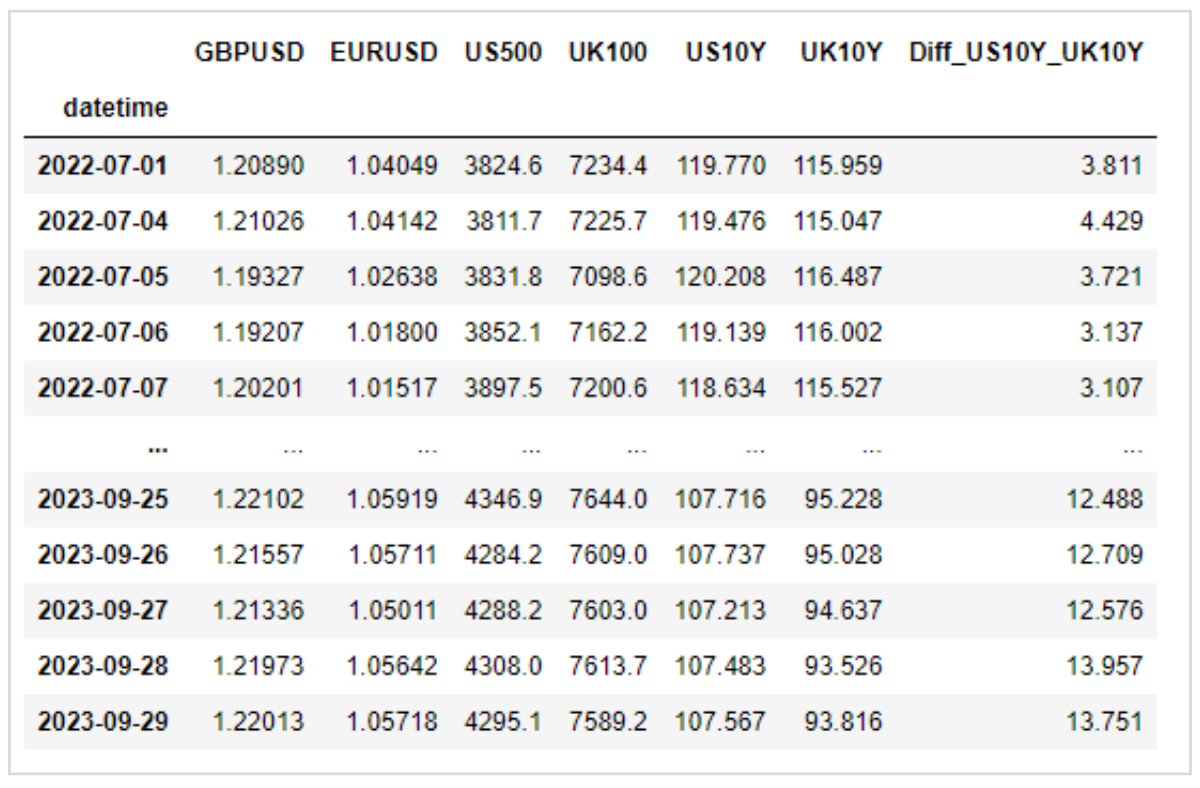
このデータを加工して、線形回帰の特徴量を作ります。
予測対象
- ● 翌日のGBPUSD
過去の値動き
- ● 前日GBPUSD
- ● 過去5日GBPUSD
- ● 過去20日GBPUSD
他シンボル
- ● 過去5日EURUSD
- ● 過去5日US500
- ● 過去5日UK100
- ● 過去5日US10Y
- ● 過去5日UK10Y
- ● 過去5日US10YとUK10Yの差
テクニカル指標
- ● SMA(5)とSMA(20)の差
- ● RSI(5)
- ● 標準偏差
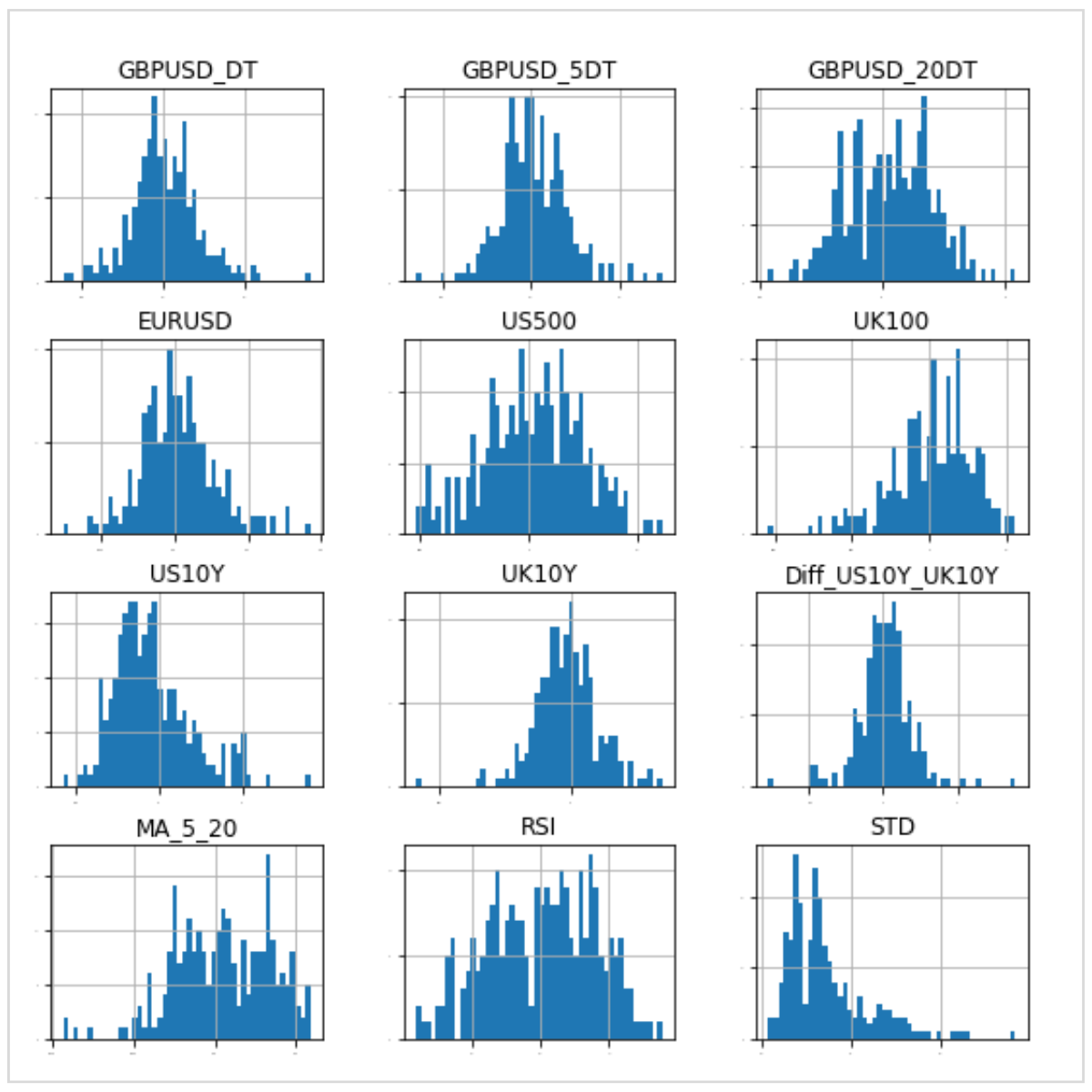
グラフは作成した12個の説明変数です。
線形回帰を実施するために、単純にこれらの説明変数の中から学習データ内の最も当てはまりの良い説明変数を選択します。
当てはまりの良さを評価するために決定係数(R-squared)を利用します。
決定係数は回帰の適合度を測る尺度です。
値が大きいほど当てはまりの良い状態で、最大値が1です。
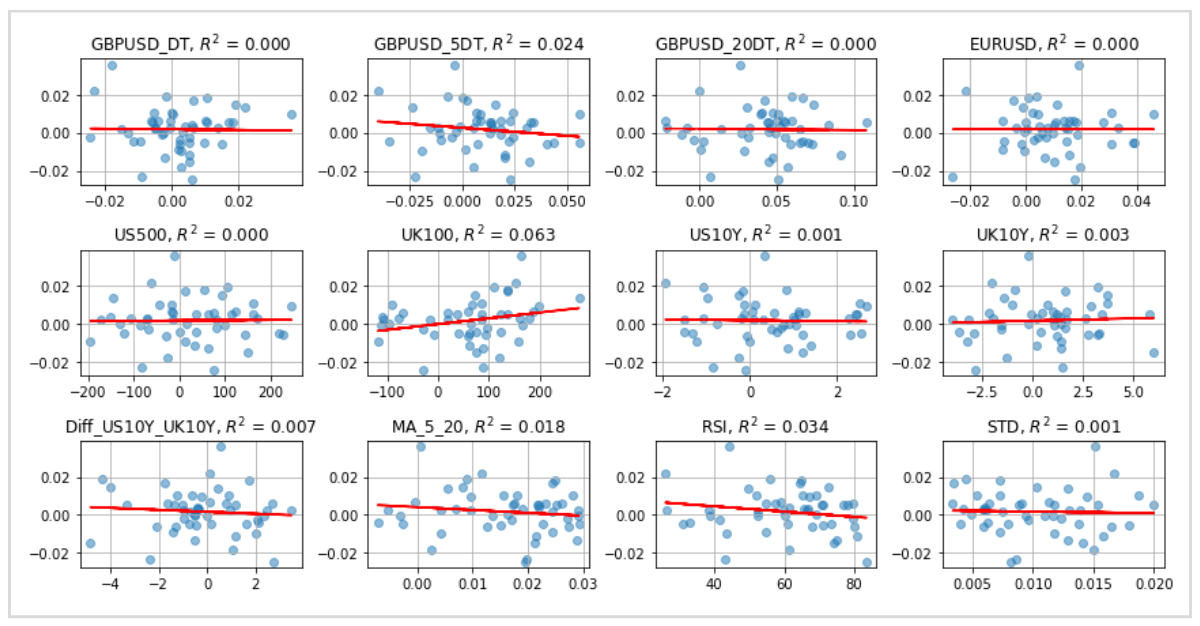
グラフは学習データのすべての説明変数にフィッティングした予測線をプロットし、グラフの上に決定係数を表示しています。
この中で最も数値が高い説明変数が、アウトオブサンプルでも高い数値を出しているかが評価のポイントです。
今回はアウトオブサンプルテストに6回のウォークフォワード法を使用します。
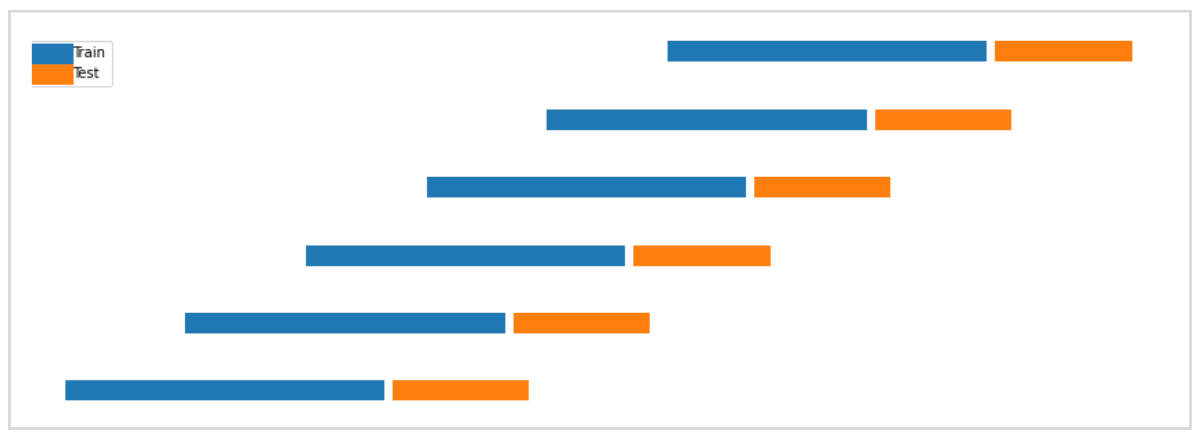
青色区間の学習データで説明変数の決定とモデルの学習を行い、学習したモデルがオレンジの区間でどれくらいの決定係数を記録するかをテストします。
以下は実際にテストした結果です。
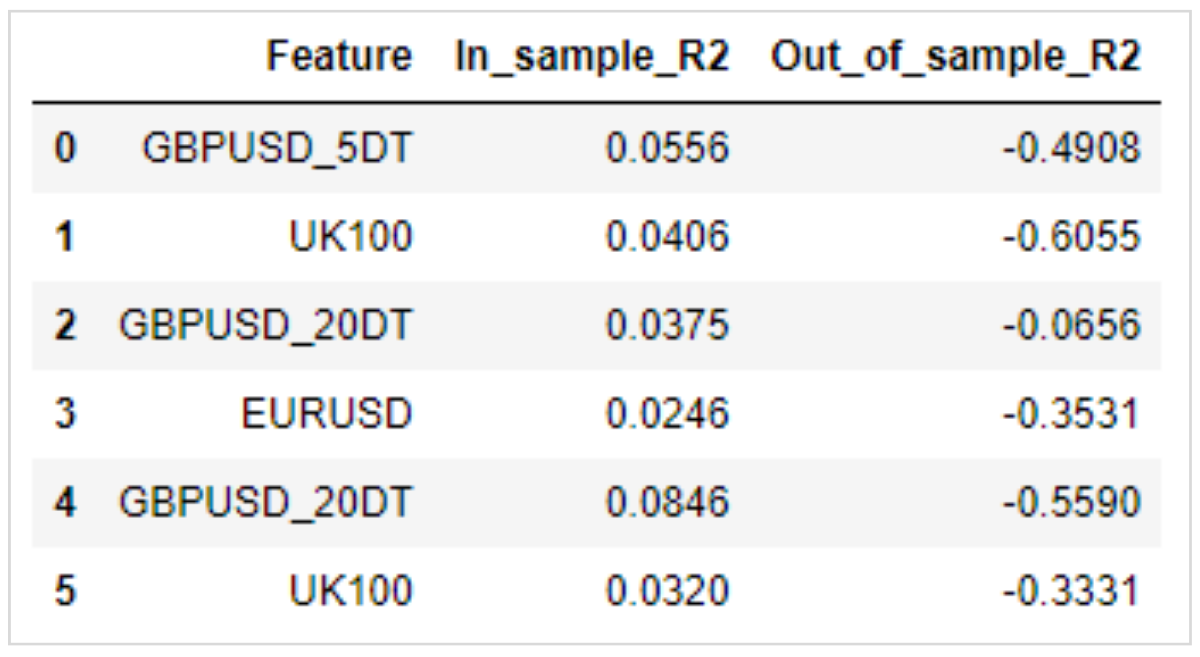
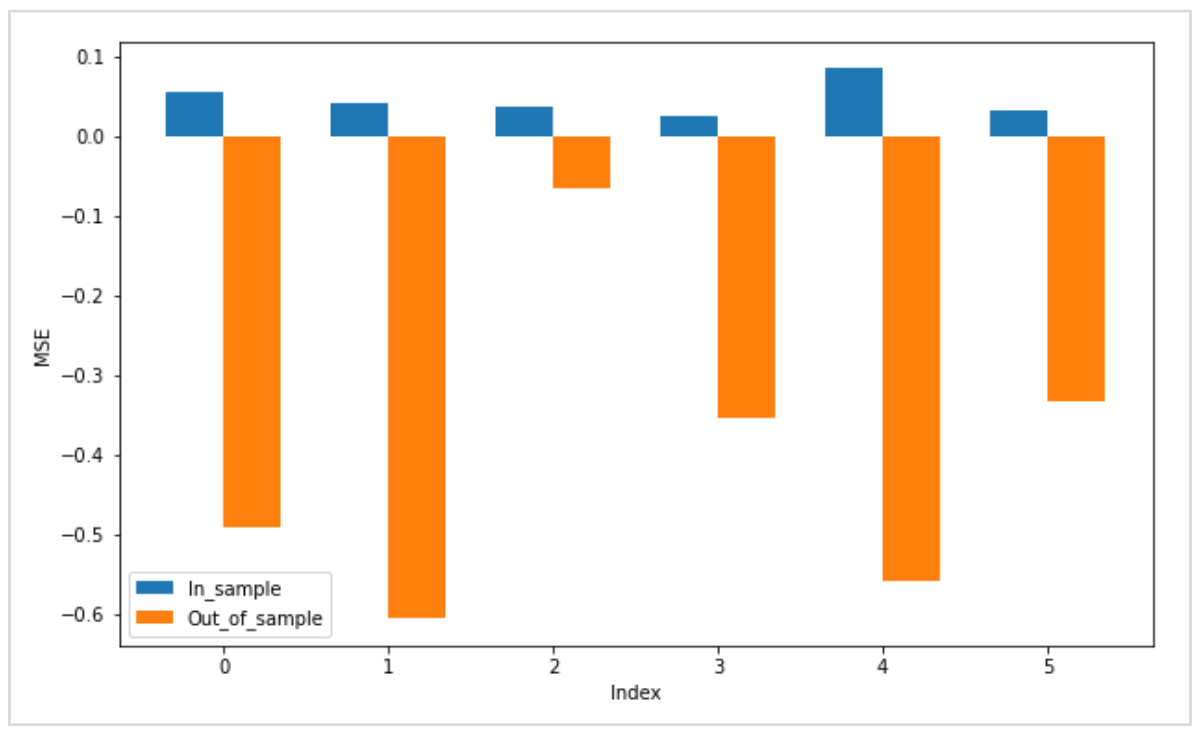
学習データ(インサンプル)とテストデータ(アウトオブサンプル)の決定係数を比較すると、テストデータが大幅に悪化し、マイナスの値を記録しています。
アウトオブサンプルの決定係数がマイナスの値を取ることは、単純な平均値よりも予測線の精度が悪かったことを意味しており、今回の設計で予測がうまくいかなかったことを示しています。
予測がうまくいかない原因は、特徴量が不適切であるときや、モデルが不適切、オーバーフィッティングなどが考えられます。
特徴量の選択や設計が、経済的に納得できる仮説に基づくものであることも望まれます。
- ● 欧州時間の初動の値動きを予測対象にする
- ● 前週高値または安値を抜けたあとの値動きを予測対象にする
- ● ファンダメンタルズ指標を特徴量にする
などアイデア次第で改善される可能性もあります(後で解説する重回帰でダミー変数を用いることで、日時データなどをカテゴリ変数として扱う分析が実装しやすくなります)。
適切な予測を行うために
上記の使用例では考慮しませんでしたが、予測の精度に関していくつか注意するポイントがあります。
ガウスマルコフの定理によると、いくつかの仮定(誤差項の不偏性、等分散性、無相関性)の下で、最小二乗法で求めたパラメータは最良線形不偏推定量というものです。
予測線と実数値との差を残差といいますが、この残差にある特性によってはガウスマルコフの定理の仮定に反する場合があり、最小二乗法を使った線形回帰が最良の結果にならない可能性があります。
系列相関
注意するポイントの一つ目は、系列相関です。
系列相関は、回帰したときの残差にある自己相関で、これがあると過去の残差の影響を考慮しない線形回帰は最良の予測になりません。
時系列データを扱うときにはとくに注意が必要です。
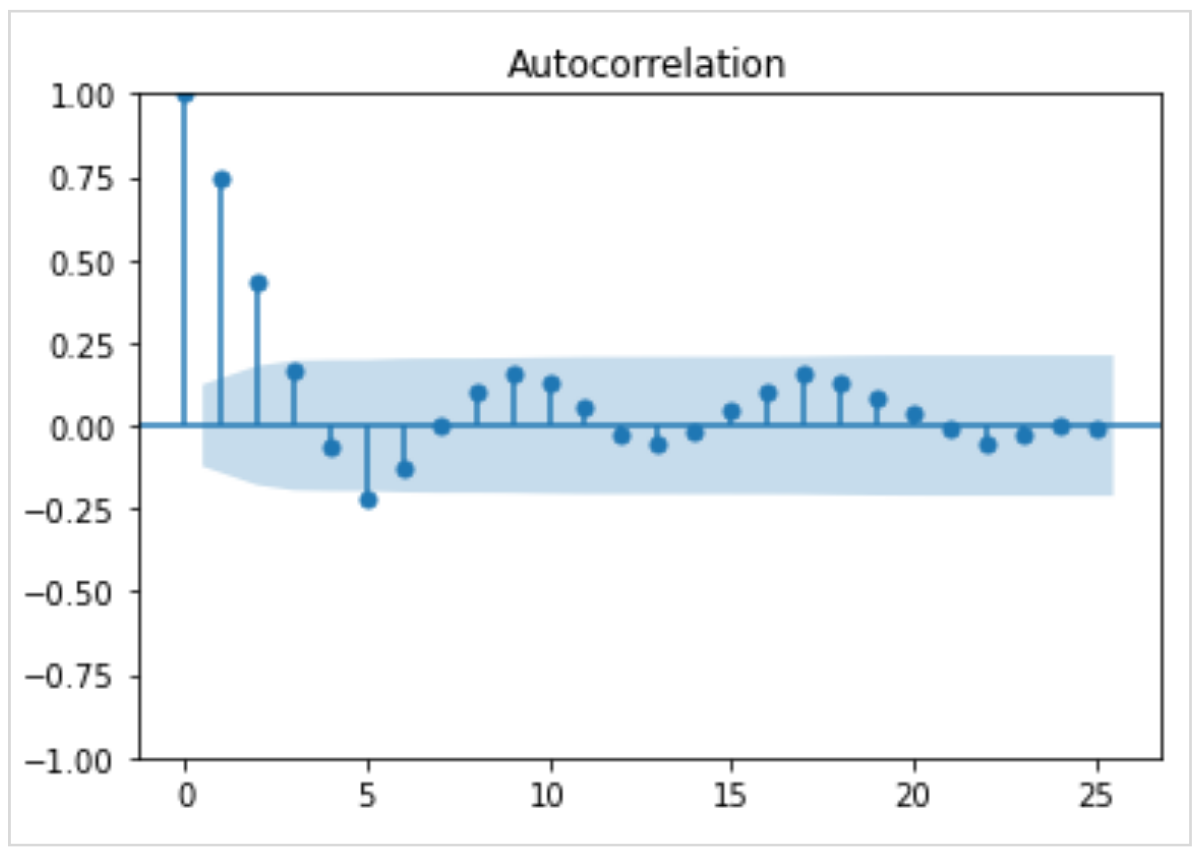
系列相関の有無をチェックするには、ダービンワトソン統計量などを利用します。
このグラフはコレログラムといい、自己相関の有無を視覚的にチェックするときに用います。
分散の不均一性
もう一つ注意したいのが分散の不均一性です。
下のグラフは残差を時系列に並べて描画したもので、ばらつき具合が時間とともに変化していく様子が確認できます。
このように残差の分散が常に一定ではなく不均一であるときも、ガウスマルコフの定理の仮定に反するので望ましい状況ではありません。
こちらは、Breusch-PaganテストやWhiteテストで診断できます。
多項式回帰
ここまで解説した線形回帰は、予測線をすべて直線で表現しました。
式はM次の関数を示しています。
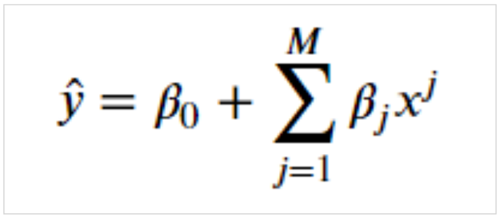
グラフは左が1次関数、右が2次関数で予測線を描画しています。
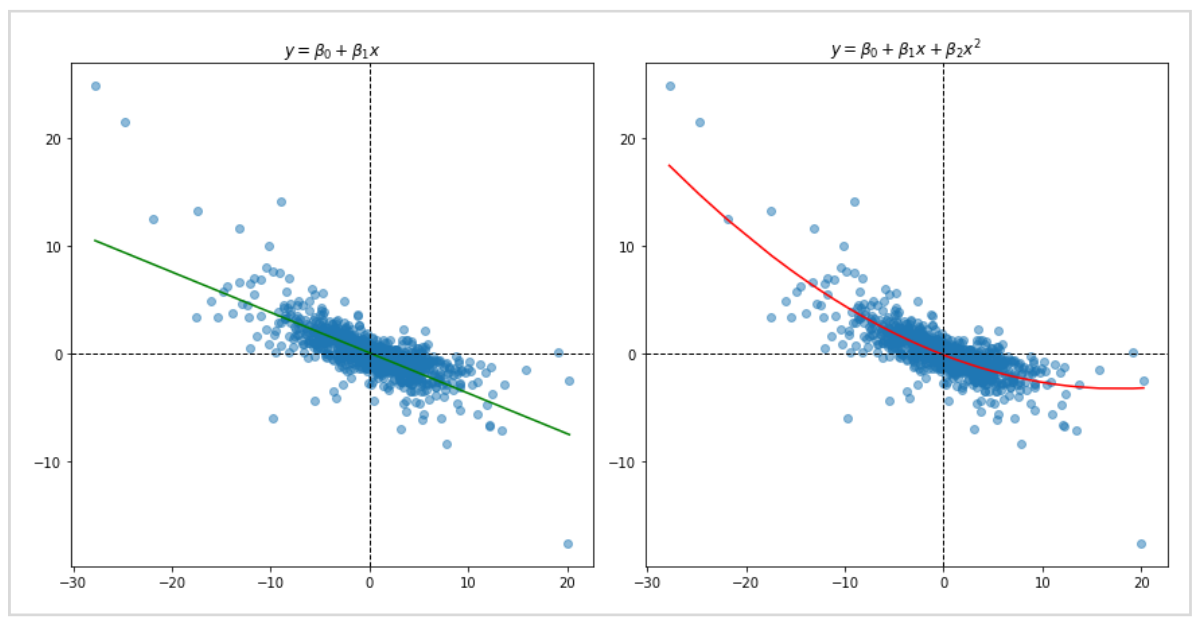
データの特徴によっては直線ではうまく予測できないこともあり、扱うデータに応じて使い分ける必要があります。
多項式回帰のパラメータを増やして複雑にしすぎると、過学習(オーバーフィッティング)を招くので注意が必要です(過学習への対策についても記事の後半で説明しています)。
重回帰
ここまで説明した線形回帰は、一つの説明変数で目的関数を予測するものです。
先ほどの例では、複数の説明変数の候補を用意していますが、決定係数が最大となる説明変数を一つ選んで線形回帰するものでした。
これに対して重回帰は、複数の説明変数で予測を行います。
一つ選ぶのではなく、すべて予測に使います。
式はp個の説明変数の重回帰を示しています。
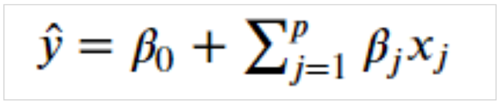
実際には予測したいデータが一つの変数にだけ依存することはあまりなく、複数の変数が複雑に影響し合っていることが多いと考えられるので、重回帰のように複数の入力を持つモデルが役立ちます。
ダミー変数
回帰は数値データ(説明変数)から数値データ(目的変数)を予測するものですが、数値データではないカテゴリ変数も扱えます。
例えば日付から曜日と月のデータを説明変数にしたいとき、これらのデータを0か1で表現するダミー変数に変換します。
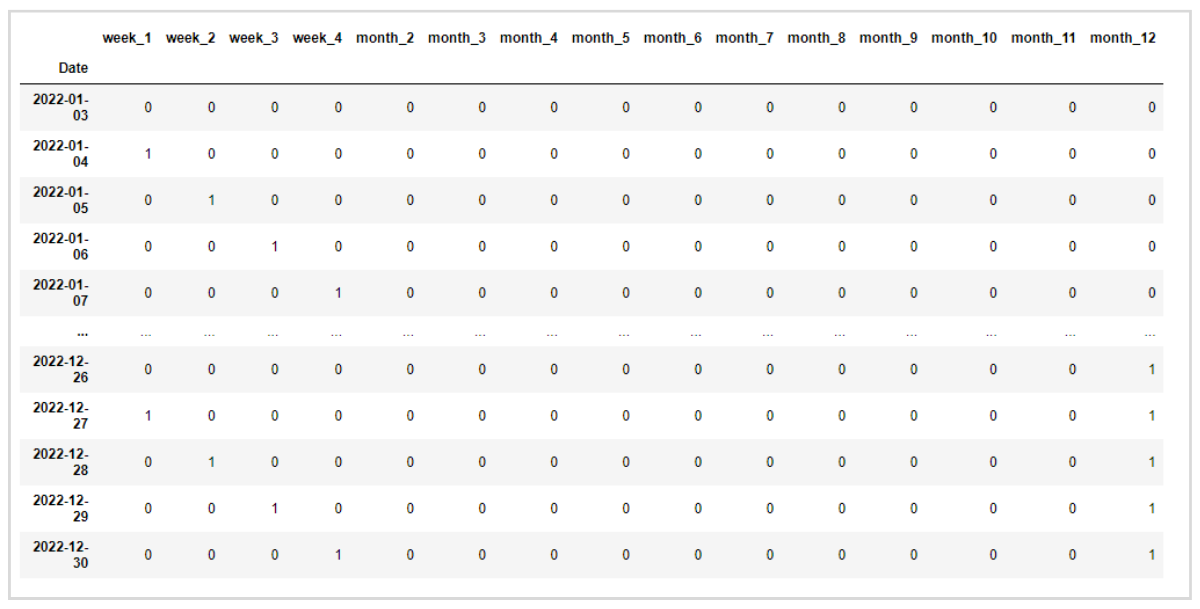
このダミー変数を重回帰の説明変数に追加することで、曜日と月の影響(季節性)を考慮して予測することが可能です。
多重共線性
重回帰を実施するときは、多重共線性というものに注意する必要があります。
複数の説明変数同士に高い相関があるとき、予測精度が悪化する問題のことです。
グラフは多重共線性を視覚的に見つけるための説明変数の相関行列と散布図行列です。
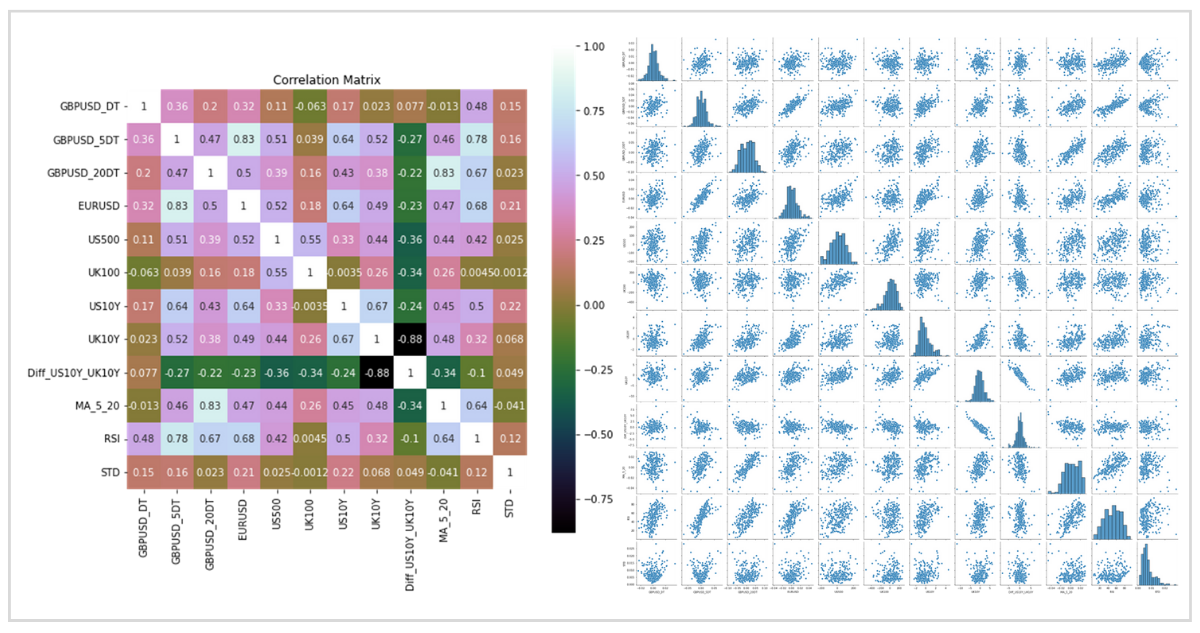
VIFという指標を確認して多重共線性の疑いを発見することが可能です。
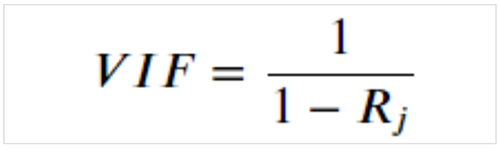
Rは説明変数同士で回帰したときの決定係数です。
一般的にVIFが10を超えると多重共線性の疑いがあるとされます。
その場合は、説明変数を削減するなどの対応を取る方が、いい結果になる可能性があります。
正則化(リッジ回帰、ラッソ回帰)
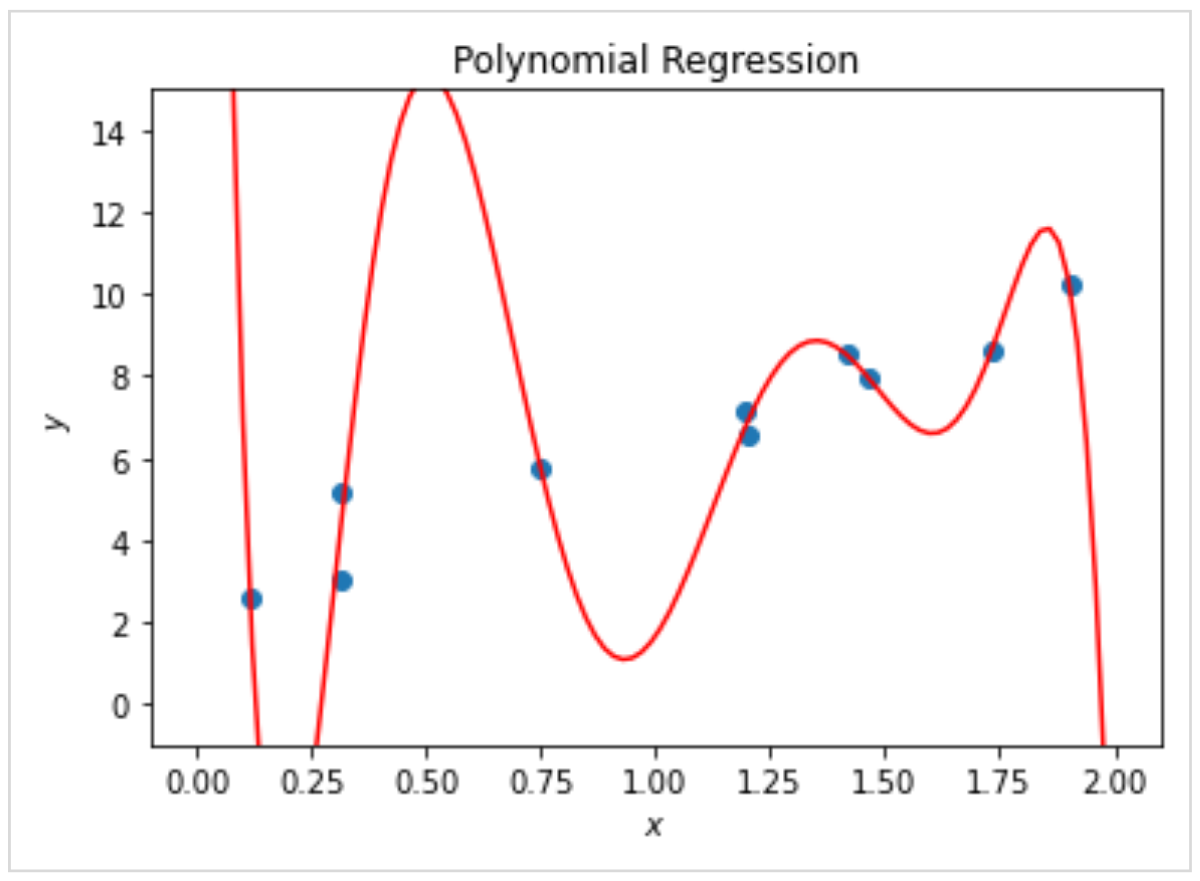
グラフは多項式回帰で学習させたモデルですが、予測線はデータの傾向を捉えておらず、無理やりにデータの上を通過するような形状をしています。
つまり、モデルが複雑すぎて過学習を起こしている状態で、予測モデルとしては使い物になりません。
過学習を避けるために、モデルの係数βが大きくなりすぎることで過学習がおこるのですが、係数βにペナルティを設けて、これを防ぐことを正則化といいます。
これはリッジ回帰の係数βを示す式です。
λはハイパーパラメータとなっています。
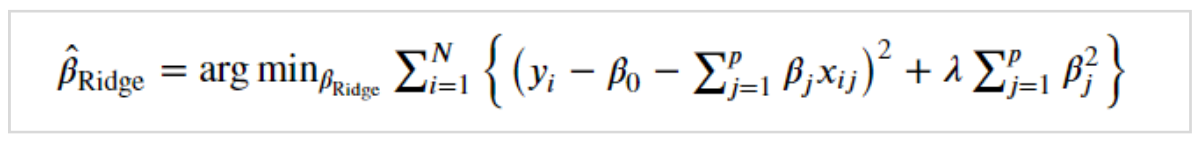
通常の線形回帰は各データと予測線との距離が最短になるように、予測線のパラメータを最適化するものでした。
言い換えれば、残差平方和が最小となるパラメータにしていることです。
対してリッジ回帰は、残差平方和にλをかけた係数の二乗和が最小となるパラメータにしています。
残差平方和が小さくなっても、係数βが大きすぎると追加されたペナルティによって全体が最小になるとは限りません。
ラッソ回帰も考え方は同じで、大きな違いはないですがペナルティの与え方に違いがあります。
λはハイパーパラメータとなっています。
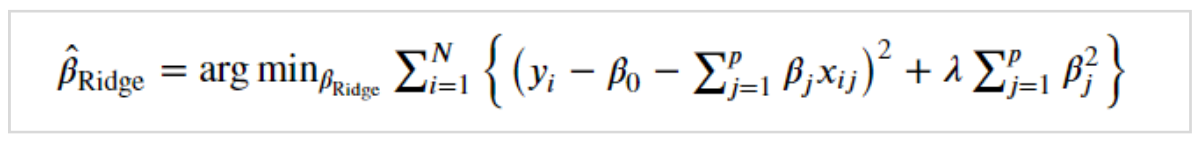
ラッソ回帰は、係数βの絶対値の和がペナルティとなっています。
同一のデータに多項式回帰、リッジ回帰、ラッソ回帰それぞれの回帰線を並べて比較します。
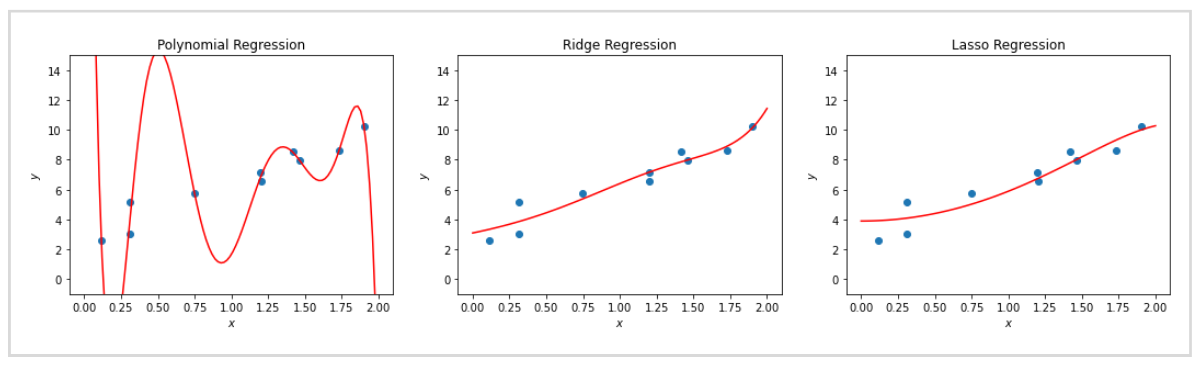
多項式回帰は過学習しているのに対して、リッジ回帰とラッソ回帰はそれを防げていることがわかります。
実際のデータで回帰を行うときには、学習データとテストデータに分けて検証しますが、学習データのスコアとテストデータのスコアが違いすぎる、つまり過学習を起こしているようなときに正則化が役に立つ可能性があります。
Provided by
藍崎@システムトレーダー
個人投資家としてEA開発&システムトレード。
トレードに活かすためのデータサイエンス / 統計学 / 数理ファイナンス / 客観的なデータに基づくテクニカル分析 / 機械学習 / MQL5 / Python
EA(自動売買)を学びたい方へオススメコンテンツ

OANDAではEA(自動売買)を稼働するプラットフォームMT4/MT5の基本的な使い方について、画像や動画付きで詳しく解説しています。MT4/MT5のインストールからEAの設定方法までを詳しく解説しているので、初心者の方でもスムーズにEA運用を始めることが可能です。またOANDAの口座をお持ちであれば、独自開発したオリジナルインジケーターを無料で利用することもできます。EA運用をお考えであれば、ぜひ口座開設をご検討ください。
本ホームページに掲載されている事項は、投資判断の参考となる情報の提供を目的としたものであり、投資の勧誘を目的としたものではありません。投資方針、投資タイミング等は、ご自身の責任において判断してください。本サービスの情報に基づいて行った取引のいかなる損失についても、当社は一切の責を負いかねますのでご了承ください。また、当社は、当該情報の正確性および完全性を保証または約束するものでなく、今後、予告なしに内容を変更または廃止する場合があります。なお、当該情報の欠落・誤謬等につきましてもその責を負いかねますのでご了承ください。