エリオット波動解説(第三回)全ての波動はより大きな波動の一部の具体例
第二回では「全ての波動はより大きな波動の一部」であることを書きました。これは具体的にはどういうことであるのかじっくりと説明したいと思います。
まず、次のようなインパルス波形の波動が出たとします。
図17

エリオット波動原理では、i ii iii iv vと5つの波動が出てインパルスが完成すると次のように1回り大きな(i)という波動になると考えます。
図18
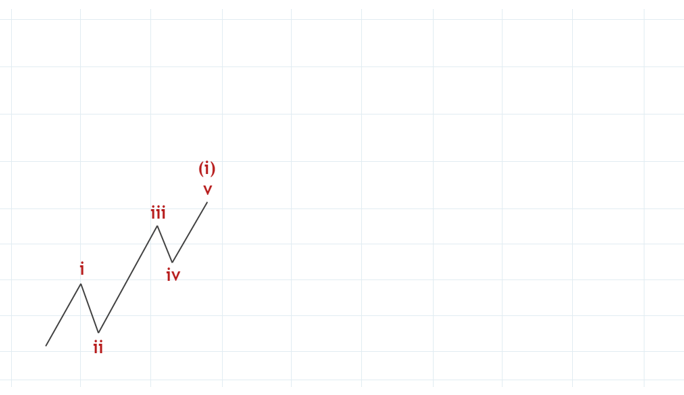
(i)が完成したのですから、続くのは(ii)ということになります。
図19
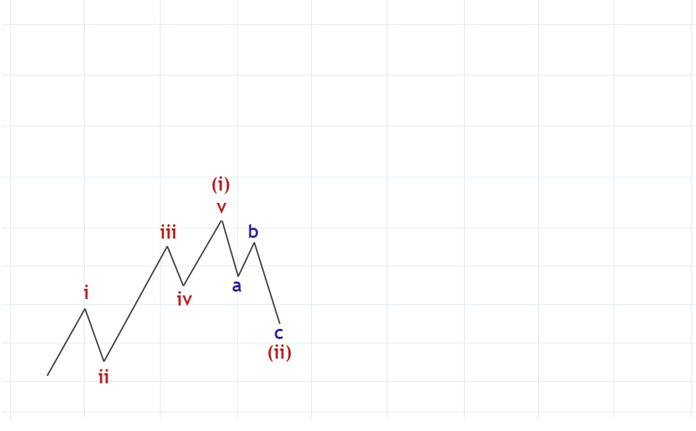
ここで(ii)波は(i)という動きに対する反動のようなものです。エリオット波動原理では(ii)波は(i)波を修正した(correction)と言います。では、(ii)の後にはどのような波が続くでしょうか。
図20
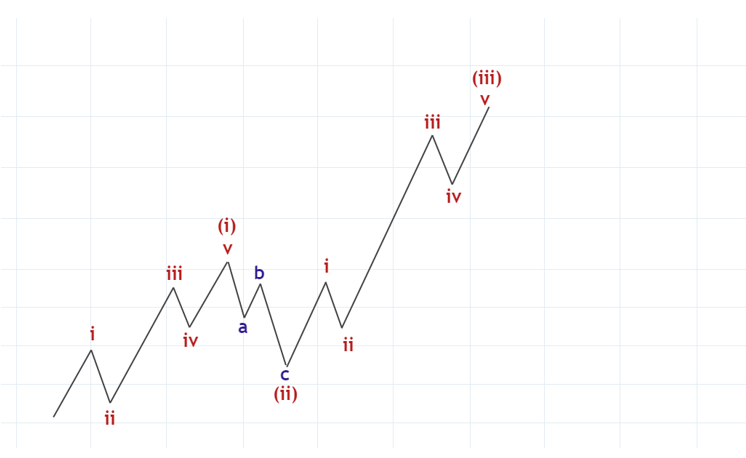
大きなインパルスを形成中であると仮定すれば、(ii)の後にはこのように(iii)波が続くことになります。その後は(iii)に対する修正としての(iv)波が出て、
図21、図22
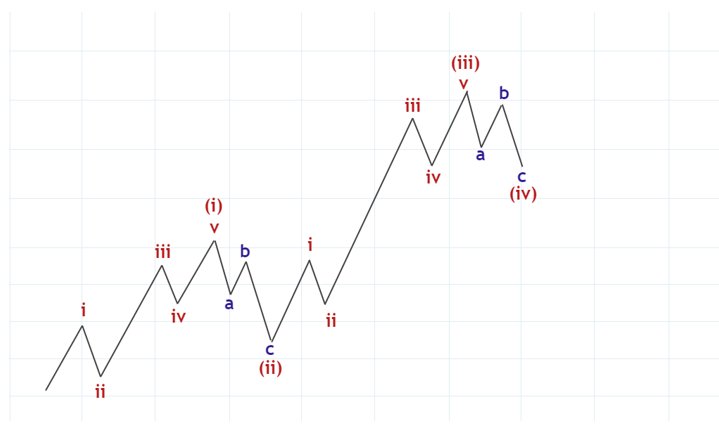
続いて(v)波が出ます。

問題はこの次です。(v)に対する修正が次のように起きるのでしょうか。
図23
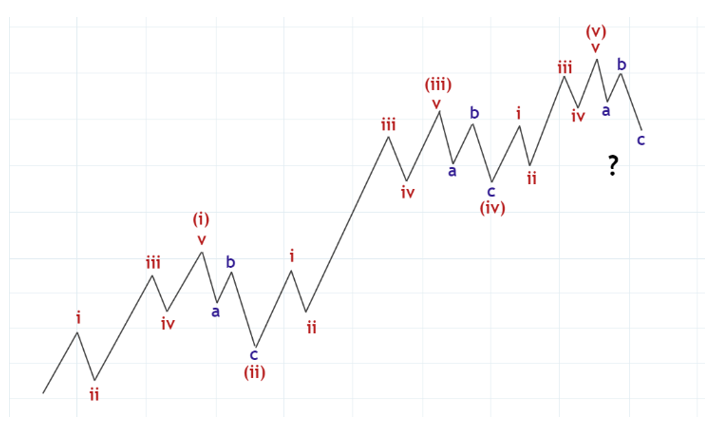
残念ながら(v)に対する修正は起きません。なぜなら(i)(ii)(iii)(iv)(v)まで完成するとその5波動がまとまって、一回り大きな階層の波動である1波になるからです。そして、その1波に対して2波という修正が起きるのです。図18のところで説明したことと同じことが繰り返されるのです。
図24
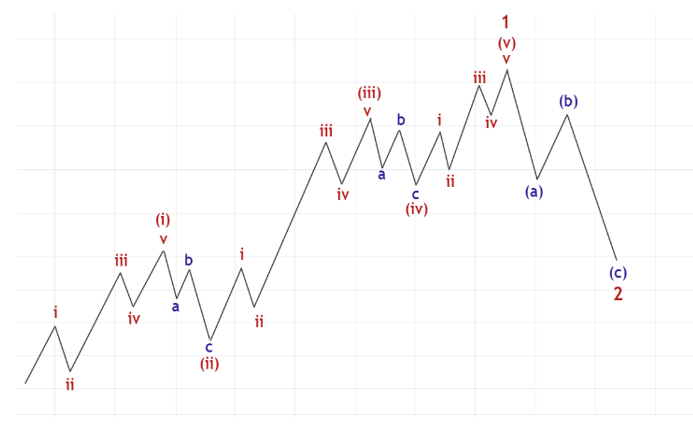
上の図には3つの階層の波動が描かれています。ローマ数字小文字のi ii iii iv vで示された波動、それに( )が付いた(i)(ii)(iii)(iv)(v)で示された波動、さらにアラビア数字の1、2で示された波動です。エリオット波動原理ではこのような階層のことをディグリーと言います。
ここで、第一回のインパルスを思い出してください。インパルスの1波、3波、5波には推進波が出て、2波と4波には修正波が出ると書いてありましたね。それを確認しながら図24を見ると、推進波を構成する波動は数字の記号が振ってあり、修正波を構成する波動にはローマ字の記号が振ってあることにお気づきだと思います。
このように、波動に記号を振ることを「ナンバリング」または「カウント」と言いますが、推進波を構成する波動には数字の記号を、修正波を構成する波動にはローマ字の記号を振るルールになっています。そして、同じディグリーの波動には同じ種類の記号を必ず振ります。図24では、(i)波と(a)波は同じディグリーということになります。
ディグリーには次の表にあるようにその大きさによって名前と記号の種類がおおよそ決まっています。
図25

※「あなたのトレード判断能力を大幅に鍛える エリオット波動研究 パンローリング刊」P43より抜粋
しかし、実際にその波動がどの大きさのディグリーであるかの確定は難しく、あくまで暫定的な判断でナンバリングすることになります。また、記号も同じディグリーの波動には同じ記号を使うということさえ守っていれば分析者が使いやすい任意の記号を使って構いません。
あるディグリーの波動がどれくらいの期間続くのかを明確に示すことはできません。一般にスーパーサイクル級の波動は数十年の期間続くと考えられていますが、約3年間しかなかった世界大恐慌による修正波はスーパーサイクル級と解釈されています。また、おおよそですが1分足チャートで目視できる最小のインパルスはミニスキュール級の波動であることが多いようです。
では、話を続けましょう。
図24をよく見ると次のように紫で囲んだ部分と、青で囲んだ部分が同じ形をしていることに気が付きます。
図26
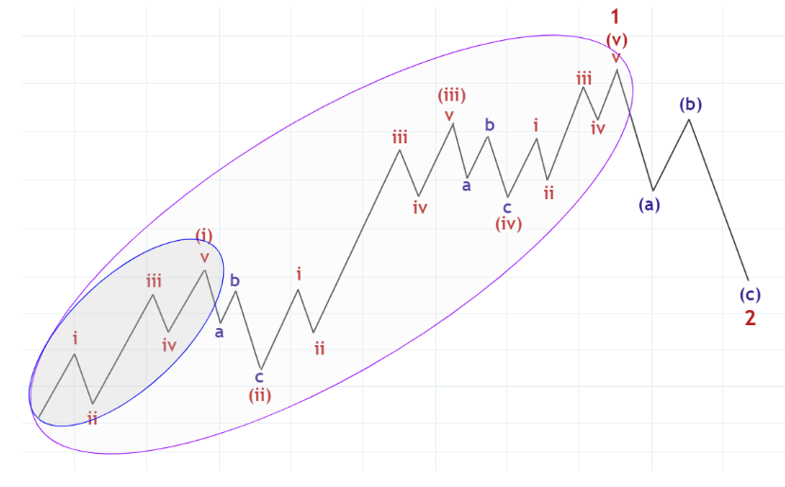
さらに図24には書いてありませんでしたが、次のように(i)波のi波もよく見ると赤で囲んだような推進波になっているはずなのです。
図27
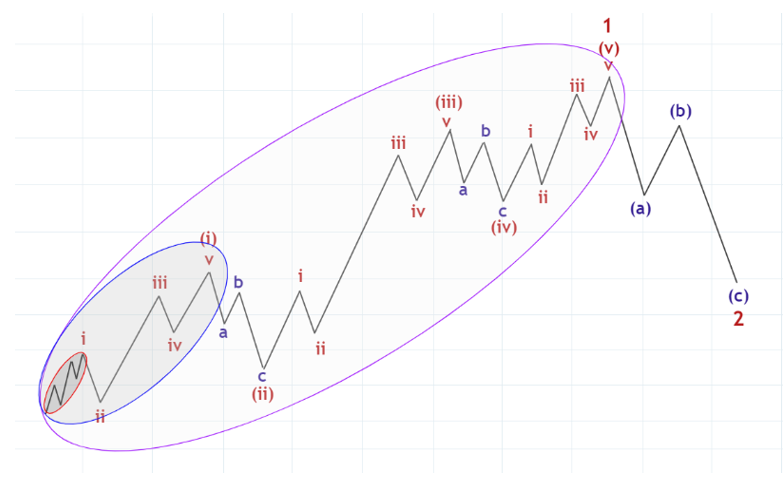
このように部分と全体が同じ形をしていることを「フラクタル」と言います。エリオット波動原理ではこのように波動は全てフラクタルになっていると考えます。これはエリオット波動原理の中でも最も重要な概念です。波動がフラクタルになっているということは言い換えれば、「全ての波動はより大きな波動の一部」ということになります。
では、本当に波動がフラクタルになっているのか、実際のチャートを調べてみましょう。
次のチャートは225CFDの週足です。リーマンショック後の安値を始点とした5波動のインパルスのように見える波動がすぐに見つかります。ここでインパルスと断定せずに「インパルスのように見える」と書いたのは、エリオット波動原理では一つの波動には必ず複数のカウントがあるからです。このことはエリオット波動原理を用いてチャートを分析するにあたってとても重要なセンテンスになります。後の回で詳しく説明します。
ここでは暫定的に次のようなインパルスであると仮定して説明します。
図28
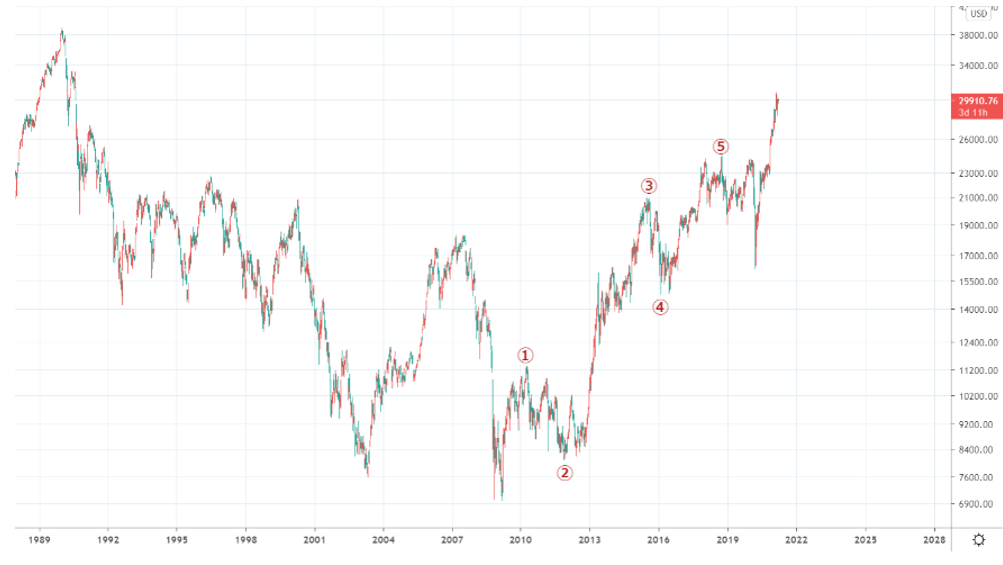
また、その③波部分は次のようなインパルスとカウントできます。
図29(日足)
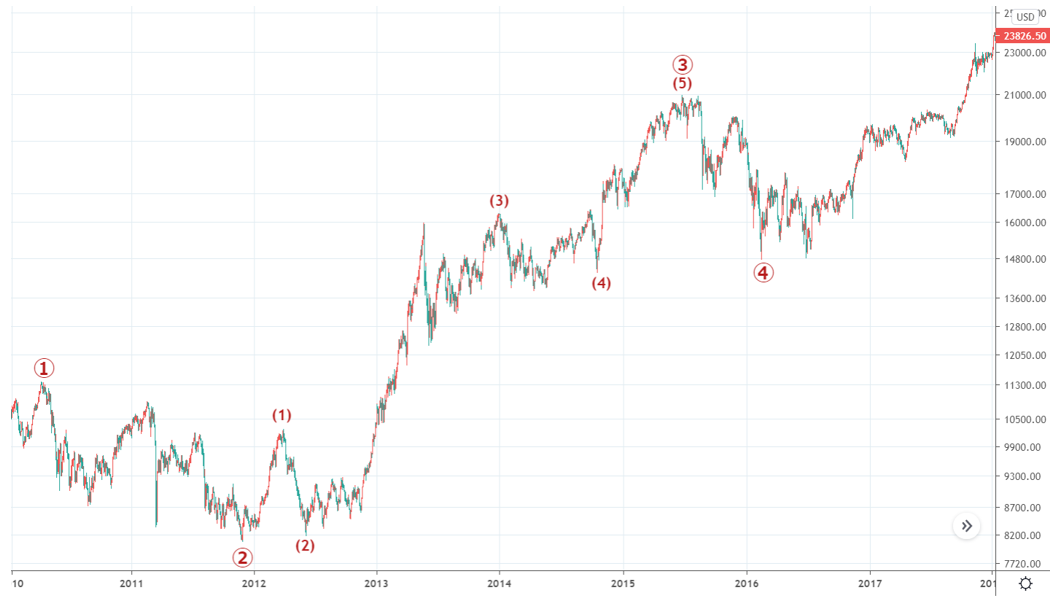
さらに、(3)の部分は次のような波動構成になっているとカウントできます。
図30(日足)
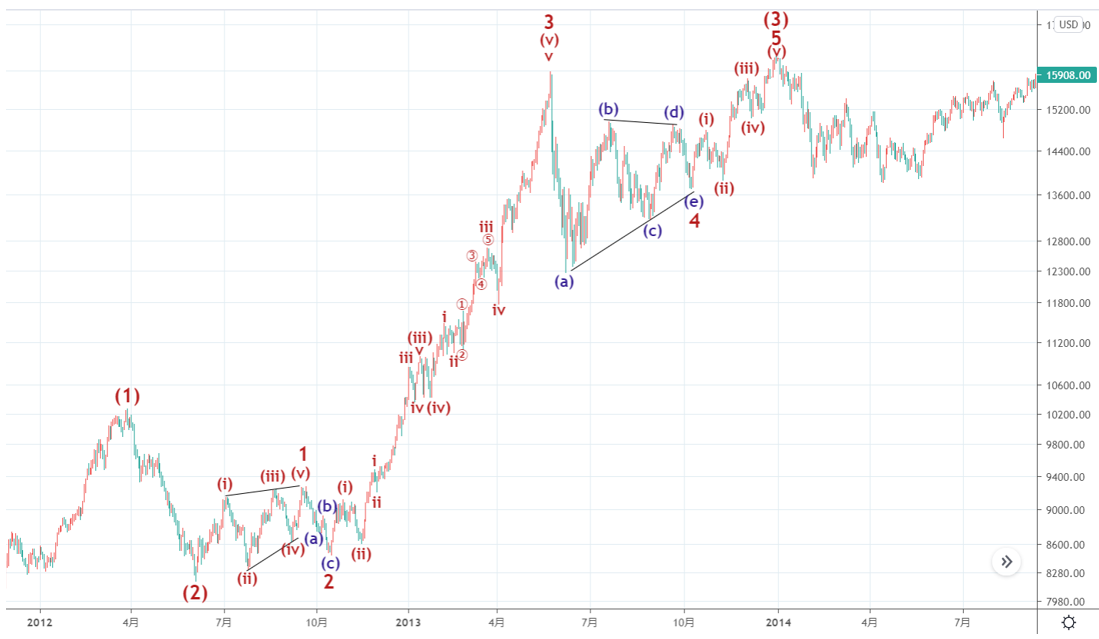
ここまでで、①②③④⑤という波動で構成された大きなインパルスがあり、そのうちの③波は(1)(2)(3)(4)(5)という波動で構成されたインパルスであり、その(3)も1 2 3 4 5という波動で構成されたインパルスであり、さらに3も(i)(ii)(iii)(iv)(v)という波動で構成されたインパルスであり、その(v)もi ii iii iv vという波動で構成されたインパルスであり、そのiiiも小さな①②③④⑤という波動で構成されたインパルスであることが分かります。
このチャートは日足チャートですが、これを1時間足、15分足、1分足へと拡大していっても同じように全ての波動がエリオット波動原理で規定された波形によって構成されているのです。これがエリオット波動原理における「フラクタル」という概念の意味です。ちょっと信じ難いですが、換言すれば、フラクタルになっていないチャートはエリオット波動原理での分析対象外であるとも言えます。
第三回はここまでになります。
※記事中のチャートにある波動カウントは一例に過ぎません。エリオット波動原理では一つのチャートに対して必ず複数のカウント案が存在しどのカウントが正しいかは事後的にしか分からず波動の進行によってカウント案自体も更新されていきます。
一般社団法人エリオット波動研究所代表理事 有川和幸氏監修
この記事を監修してくださった有川和幸氏と小泉秀希氏の共著「あなたのトレード判断能力を大幅に鍛えるエリオット波動研究 基礎からトレード戦略まで網羅したエリオット波動の教科書(パンローリング社) 」には更に詳しくエリオット波動について説明されています。
エリオット波動についてもっと学びたい方へのオススメ

一般社団法人エリオット波動研究所代表理事の有川和幸(ありかわかずゆき)氏監修のもとエリオット波動の基本的な知識や使い方、トレーディングアイデアなどをご紹介。またエリオット波動へ応用が可能なOANDAオリジナル・インジケーター「OANDA_Auto_fibonacci(オート・フィボナッチ)」を無料配布中。このインジケーターはOANDAの口座をお持ちのお客様だけがお使いいただけます。
本ホームページに掲載されている事項は、投資判断の参考となる情報の提供を目的としたものであり、投資の勧誘を目的としたものではありません。投資方針、投資タイミング等は、ご自身の責任において判断してください。本サービスの情報に基づいて行った取引のいかなる損失についても、当社は一切の責を負いかねますのでご了承ください。また、当社は、当該情報の正確性および完全性を保証または約束するものでなく、今後、予告なしに内容を変更または廃止する場合があります。なお、当該情報の欠落・誤謬等につきましてもその責を負いかねますのでご了承ください。











